Description
In medical images, noise suppression is a particularly delicate and difficult task. A trade off between noise reduction and the preservation of actual image features has to be made in a way that enhances the diagnostically relevant image content. Image processing specialists usually lack the biomedical expertise to judge the diagnostic relevance of the denoising results. For example, in ultrasound images, speckle noise may contain information useful to medical experts [39]; the use of speckled texture for a diagnosis was discussed in [18] and [35]. Also, biomedical images show extreme variability and it is necessary to operate on a case by case basis [36]. This motivates the construction of robust and versatile denoising methods that are applicable to various circumstances, rather than being optimal under very specific conditions. The notion of robustness in multiscale denoising was addressed in [19]. In this paper, we propose one robust method that adapts itself to various types of image noise as well as to the preference of the medical expert: a single parameter can be used to balance the preservation of (expert-dependent) relevant details against the degree of noise reduction.
In image denoising, one often faces uncertainty about the presence of a given “feature of interest” (e.g., an image edge) in a noisy observation. Due to the sparsity of the wavelet representation, the Middleton’s optimum coupled detection and estimation approach [28] seems well suited for wavelet domain image denoising. To the authors’ knowledge such approaches have received little attention so far in wavelet domain filtering. Bayesian methods [2], [5], [37] take the uncertainty of the signal presence into account implicitly, assuming a Bernoulli process on the wavelet coefficients [20] and using Gaussian mixture models for the probability density functions of the wavelet coefficients. Related hereto, but more sophisticated, spatially adaptive methods usually employ complex algorithms, based on hidden Markov tree models [6], [10] or Markov random field prior models [17], [23], [31]. Other recent trends in wavelet-based image denoising include applying different types of filtering in supposedly smooth and supposedly heterogeneous or “edged” image regions [12], [21], spatially adaptive thresholding [4] and locally adaptive Wiener filtering [29].
outputs of MATLAB Code :
peaksnr before = 23.68
snr before = 13.80
peaksnr after = 27.809641756910743
snr after = 17.936949104490768
ssimValues before = 0.221784578748779
ssimValues after = 0.464511041250099
input image
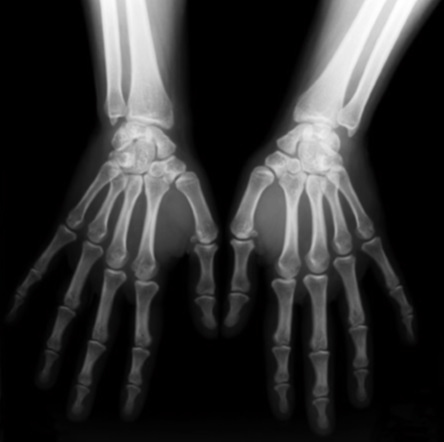
noisy image

denoised image :

second input image :

noisy image :

denoised image :

REFERENCES
[1] T. Aach and D. Kunz, “Anisotropic spectral amplitude estimation for noise reduction and image enhancement,” in Proc. IEEE Int. Conf. Image Processing, Lausanne, Switzerland, 1996, pp. 335–338.
[2] F. Abramovich, T. Sapatinas, and B. W. Silverman, “Wavelet thresholding via a Bayesian approach,” J. Roy. Statist. Soc. B, vol. 60, pp. 725–749, 1998.
[3] A. Achim, A. Bezerianos, and P. Tsakalides, “Novel Bayesian multiscale method for speckle removal in medical ultrasound images,” IEEE Trans. Med. Imag., vol. 20, pp. 772–783, Aug. 2001.
[4] S. G. Chang, B. Yu, and M. Vetterli, “Spatially adaptive wavelet thresholding with context modeling for image denoising,” IEEE Trans. Image Processing, vol. 9, pp. 1522–1531, Sept. 2000.
[5] H. A. Chipman, E. D. Kolaczyk, and R. E. McCulloch, “Adaptive Bayesian wavelet shrinkage,” J. Amer. Statist. Assoc., vol. 92, pp. 1413–1421, 1997.
[6] M. S. Crouse, R. D. Nowak, and R. G. Baranuik, “Wavelet-based statistical signal processing using hidden Markov models,” IEEE Trans. Signal Processing, vol. 46, pp. 886–902, Apr. 1998.
[7] D. L. Donoho, “De-noising by soft-thresholding,” IEEE, Trans. Inform. Theory, vol. 41, pp. 613–627, May 1995.
[8] W. A. Edelstein, G. Glover, C. Hardy, and R. Redington, “The intrinistic signal-to-noise ratio in NMR imaging,” Magn. Reson. Med., vol. 3, pp. 604–618, 1986.
[9] Y. Ephraim and D. Malah, “Speech enhancement using a minimum mean-square error short-time spectral amplitude estimation,” IEEE Trans. Acoust. Speech Signal Processing, vol. ASSP-32, pp. 1109–1121, Dec. 1984.
[10] G. Fan and X.-G. Xia, “Image denoising using local contextual hidden markov model in the wavelet domain,” IEEE Signal Processing Lett., vol. 8, pp. 125–128, May 2001.
[11] S. Foucher, G. B. Benie, and J. M. Boucher, “Unsupervised multiscale speckle filtering,” in Proc. IEEE Int. Conf. Image Processing, Lausanne, Switzerland, 1996, pp. 391–394.
[12] , “Multiscale MAP filtering of SAR images,” IEEE Trans. Image Processing, vol. 10, pp. 49–60, Jan. 2001.
[13] J.W. Goodman, “Some fundamental proprerties of speckle,” J. Opt. Soc. Amer., vol. 66, pp. 1145–1150, 1976.
[14] H. Gudbjartsson and S. Patz, “The Rician distribution of noisy MRI data,” Magn. Reson. Med., vol. 34, pp. 910–914, 1995.
[15] T.-C. Hsung, D. P.-K. Lun, and W.-C. Siu, “Denoising by singularity detection,” IEEE Trans. Signal Processing, vol. 47, pp. 3139–3144, Nov. 1999.
[16] A. K. Jain, Fundamental of Digital Image Processing. Upper Saddle River, NJ: Prentice-Hall, 1989.
[17] M. Jansen and A. Bultheel, “Geometrical priors for noisefree wavelet coefficient configurations in image de-noising,” in Bayesian Inference inWavelet Based Models, P. Müller and B. Vidakovic, Eds. New York: Springer-Verlag, 1999, pp. 223–242.
[18] G. Kossof, W. J. Garret, D. A. Carpenter, J. Jellins, and M. J. Dadd, “Principles and classification of soft tissues by gray scale echography,” Ultrasound Med. Biol., vol. 2, pp. 89–105, 1976.
[19] H. Krim and I. C. Schick, “Minimax description length for signal denoising and optimized representation,” IEEE Trans. Inform. Theory, vol. 45, pp. 898–908, Apr. 1999.
[20] D. Leporini, J.-C Pasquet, and H. Krim, “Best basis representation with prior statistical models,” in Lecture Notes in Statistics, P. Müller and B. Vidakovic, Eds. New York: Springer-Verlag, 1999, pp. 155–172.
[21] X. Li and M. Orchard, “Spatially adaptive denoising under overcomplete expansion,” presented at the IEEE Int. Conf. Image Processing, Vancouver, BC, Canada, Sept. 2000.
[22] A. Macovski, “Noise in MRI,” Magn. Reson. Med., vol. 36, pp. 494–497, 1996.
[23] M. Malfait and D. Roose, “Wavelet-based image denoising using a Markov random field a priori model,” IEEE Trans. Image Processing, vol. 6, pp. 549–565, Apr. 1997.
[24] S. Mallat, “A theory for multiresolution signal decomposition: The wavelet representation,” IEEE Trans. Pattern Anal. Machine Intell., vol. 11, pp. 674–693, July 1989.
[25] , A Wavelet Tour of Signal Processing. New York: Academic, 1998.
[26] R. J. McAulay and M. L. Malpass, “Speech enhancement using a softdecision noise suppression filter,” IEEE Trans. Acoust. Speech Signal Processing, vol. ASSP-28, pp. 137–144, Apr. 1980.
[27] E. R. McVeigh, R. M. Henkelman, and M. J. Bronskill, “Noise and filtration in magnetic resonance imaging,” Med. Phys., vol. 3, pp. 604–618, 1985.
[28] D. Middleton and R. Esposito, “Simultaneous optimum detection and estimation of signals in noise,” IEEE Trans. Inform. Theory, vol. IT-14, pp. 434–443, May 1968.
[29] M. K. Mihçak, I. Kozintsev, K. Ramchandran, and P. Moulin, “Lowcomplexity image denoising based on statistical modeling of wavelet coefficients,” IEEE Signal Processing Lett., vol. 6, pp. 300–303, Dec. 1999.
[30] R. D. Nowak, “Wavelet-based rician noise removal for magnetic resonance imaging,” IEEE Trans. Image Processing, vol. 8, pp. 1408–1419, Oct. 1999.
[31] A. Piˇzurica, W. Philips, I. Lemahieu, and M. Acheroy, “A joint interand intrascale statistical model for Bayesian wavelet based image denoising,” IEEE Trans. Image Processing, vol. 11, pp. 545–557, May 2002.
[32] A. Piˇzurica, “Image denoising using wavelets and spatial context modeling,” Ph.D. dissertation, Ghent Univ., Ghent, Belgium, 2002.
[33] A. Piˇzurica, W. Philips, I. Lemahieu, and M. Acheroy, “Despeckling SAR images using wavelets and a new class of adaptive shrinkage functions,” in IEEE Int. Conf. Image Processing, Thessaloniki, Greece, Oct. 2001.
[34] F. Sattar, L. Floreby, G. Salomonsson, and B. Lövström, “Image enhancement based on a nonlinear multiscale method,” IEEE Trans. Image Processing, vol. 6, pp. 888–895, June 1997.
[35] F. G. Sommer, L. F. Joynt, B. A. Carroll, and A. Macowski, “Ultrasonic characterization of abdominal tissues via digital analysis of backscattered waveforms,” Radiol., vol. 141, pp. 811–817, Dec. 1981.
[36] M. Unser and A. Aldroubi, “A review of wavelets in biomedical applications,” Proc. IEEE, vol. 84, pp. 626–634, Apr. 1996.
[37] B. Vidakovic, “Wavelet-based nonparametric Bayes methods,” in Practical Nonparametric and Semiparametric Bayesian Statistics, D. D. Dey, P. Müller, and D. Sinha, Eds. New York: Springer-Verlag, 1998, Lecture Notes in Statistics 133, pp. 133–155.
[38] Y. Xu, J. B. Weaver, D. M. Healy, and J. Lu, “Wavelet transform domain filters: A spatially selective noise filtration technique,” IEEE Trans. Image Processing, vol. 3, pp. 747–758, Nov. 1994.
[39] R. F. Wagner, S. W. Smith, J. M. Sandrik, and H. Lopez, “Statistics of speckle in ultrasound B-scans,” IEEE Trans. Sonics Ultrason., vol. SU-30, pp. 156–163, May 1983.
[40] J.Weaver, Y. Xu, D. Healy, and J. Driscoll, “Filtering MR images in the wavelet transform domain,” Magn. Reson. Med., vol. 21, pp. 288–295, 1991.
Object Location and Tracking In Image Processing


Reviews
There are no reviews yet.