SVD for image compression

Description

SVD can be used as a form of image compression. The idea is to fi nd redundancies in an image, keep the most signi ficant ones and toss out the less important onces. Similar to the minimal example above, we can toss out the “noise” in an image, which may contribute signi ficantly to it’s fi le size,
but have a very small impact on the percieved quality of the image.

% Load and convert original image to grayscale

z = imread('myimg.png');

z = rgb2gray(z); % convert rgb image to grayscale

z = im2double(z); % convert image to double

figure();

imshow(z);

xlabel('Original grayscale image of z');



% Decompose into z = U*S*V'

[U,S,V] = svd(z);

% Examine sigular values

s = diag(S);

figure();

stem(s);

xlabel('n');

ylabel('S(n,n)');

title('Singular Values of z'); 

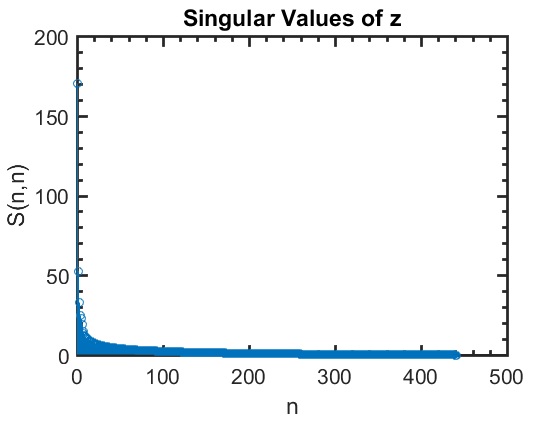
Unlike the minimal example where we knew there to be three signi ficant singular values due to the way the matrix was constructed, there is no obvious repeating pattern in most photographs, with the exception of Shayne’s head being cropped onto a copy of my body due to his absence during the time of this group picture.

We see that there are many signi ficant singular values, and no obvious cut off point. As we did above, we will choose to make a rank approximation.

% Make k'th rank approximation of the input matrix
k = 100;
Uc = U(:,1:k); % Compressed version of U

Sc = S(1:k,1:k);
Vc = V(:,1:k);
zc = Uc*Sc*Vc'; % don't forget the prime when reconstructing z
figure();
imshow(zc);
xlabel(['k = ' num2str(k) ' rank approximation of z']);

https://matlab1.com/shop/matlab-code/robust-principal-component-analysis-with-complex-noise/
http://fourier.eng.hmc.edu/e161/lectures/svdcompression.html