Description
Natural images are known to have scale invariant statistics. While some eariler studies have reported the kurtosis of marginal bandpass filter response distributions to be constant throughout scales, other studies have reported that the kurtosis values are lower for high frequency filters than for lower frequency ones. In this work we propose a resolution for this discrepancy and suggest that this change in kurtosis values is due to noise present in the image.
We suggest that this effect is consistent with a clean, natural image corrupted by white noise. We propose a model for this effect, and use it to estimate noise standard deviation in corrupted natural images. In particular, our results suggest that classical benchmark images used in low-level vision are actually noisy and can be cleaned up. Our results on noise estimation on two sets of 50 and a 100 natural images are significantly better than the state-of-the-art.
In this work we describe and explain a baffling phenomena. When measuring the kurtosis of marginal filter response distributions in natural images, in many (but not all) natural images, values of kurtosis for lower frequency filters are higher than high frequency ones. This is in contrast to the scale-invariant nature of natural images. We argue that clean, natural images should have a constant kurtosis value throughout scales, and propose that deviations from this are due to noise inherent in the image. Using this assumption we show how the noise level in a corrupted image can be accurately estimated, for a range of scene types and noise levels, and under different corruption scenarios.
A particularly intriguing example is the ubiquitous Lena image – a very common benchmark image – which we show here to be noisy. We showed that this image is noisy in its original form, and using it as “ground truth” in low-level vision experiments should be done with caution.
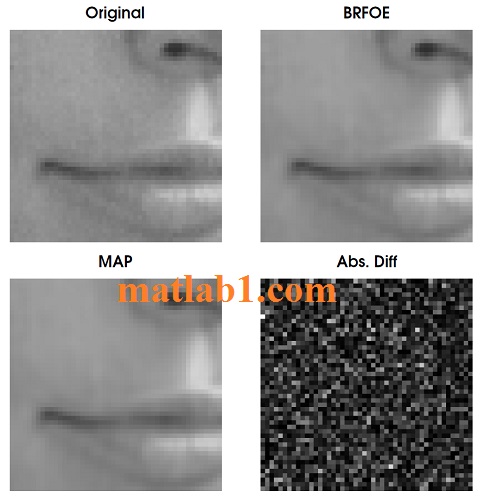
Denoising results for the original Lena image using simple scale-invariant Bayesian and BRFOE denoising. On the top left is the original image (detail), on the top right is the denoised image (BRFOE). Details are fully preserved in the denoised image, but noise is much less apparent. MAP denoising is on bottom left. Difference image is scaled, and with BRFOE image.
Zoran, Daniel, and Yair Weiss. “Scale invariance and noise in natural images.” In Computer Vision, 2009 IEEE 12th International Conference on, pp. 2209-2216. IEEE, 2009.



Reviews
There are no reviews yet.