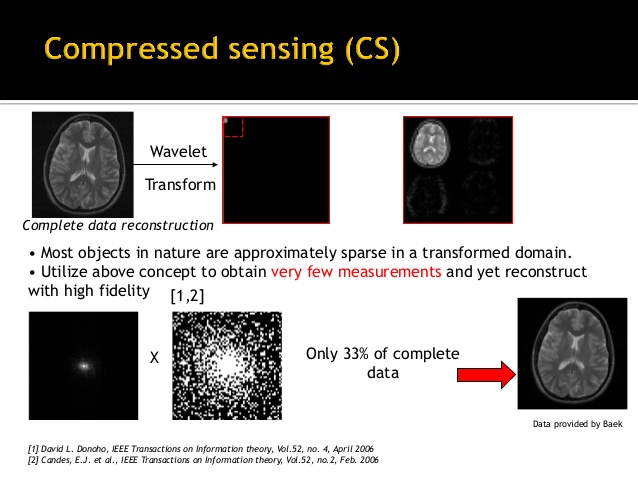
Compressed Sensing MRI
Parallel imaging has led to revolutionary progress in the field of rapid MRI in the past two decades. However, as discussed in the previous section, the maximum acceleration that can be achieved in parallel imaging is limited by the number and the design of coils, and ultimately by fundamental electrodynamic principles. Compressed sensing is another powerful approach that can be applied to accelerate data acquisitions in MRI , and has attracted enormous attention since its introduction. Compressed sensing can be combined with parallel
imaging in MRI to further increase imaging speed by exploiting joint sparsity in multicoil images. In this section, the basics of compressed sensing, its application for MRI, and its combination with parallel imaging, are briefly reviewed.
Introduction to Compressed Sensing
Conventional schemes for sampling a signal must satisfy the requirements of the Nyquist theorem: namely, that the sampling rate must be at least twice the maximum bandwidth presented in the signal. Unfortunately, in many applications, Nyquist sampling is time consuming and data-intensive, posing a challenge for sampling system design, data storage, and transmission. In order to address this logistical and computational challenge, high-dimensional
data are usually compressed after acquisition by transforming to a basis that provides a sparse or compressible representation for the signal and discarding insignificant components. This transform coding framework has been widely used in the JPEG, JPEG2000, and MPEG standards. The ability to compress images so effectively raises an interesting question, one which underlies compressed sensing: instead of first sampling a signal at a high sampling rate and then discarding most of the sampled measurements in the compression process, why not directly acquire the data in a compressed form at a lower sampling rate? In other words, can we build the compression process directly into the acquisition or sensing step, so that one does not have to
perform so many measurements and discard most of them afterwards? Candes, Romberg, Tao, and Donoho proved the feasibility of this hypothesis and proposed a framework by which a sparse or compressible signal could be successfully recovered from undersampled measurements that are far below the Nyquist limi After rapid development in the past decade, compressed sensing has already achieved notable impact in a wide range of application areas, such as sensor design in high-resolution cameras and
medical imaging. One of the applications that can substantially benefit from compressed sensing is MRI, in which the imaging speed can be dramatically improved if three requirements can be satisfied, including :
i) the image is sparse or has a sparse representation in some transform domain;
ii) incoherent sampling, seen in the structural preservation of image content and the structural disintegration of artifacts in the sparse domain;
iii) a non-linear reconstruction to recover the image by removing the incoherent artifact. The discussions in the following sections will focus on these aspects.
The Sensing Problem
The sampling of a signal vector m with size N×1 can be interpreted as a projection of the signal onto the sampling waveforms φi
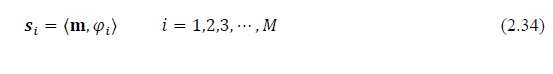
Here s is a measurement vector with size M×1. In matrix notation, we have

Here the waveforms form the sampling matrix Φ with size of M×N.
In the case of undersampling, the number of measurements is smaller than the dimensionality of the signal (M<N) and therefore the system is under-determined, assuming that the sampling matrix Φ has full rank. As shown in Section 2.5, the solution to Eq. (2.35) is not unique. However, if the signal m is known to be sparse and the sampling matrix Φ satisfies certain specific requirements, it is possible to recover the signal from an incomplete set of measurements. Suppose a signal has K significant components in M total elements, K<M. In this case, the measurement matrix Φ can be reduced to ΦK, with size M×K, by keeping only the K columns corresponding to nonzero locations. The signal m can be similarly reduced to  with only the significant coefficients. Therefore, the system becomes
with only the significant coefficients. Therefore, the system becomes

where e represents the noise. In this situation, only K measurements are sufficient to recover the signal.
Sparsity
A signal is said to be sparse if it only contains few significant coefficients. A signal is compressible if it is sparse in some transform domain. Mathematically, a compressible signal m can be expanded in a transform basis (such as a wavelet basis) ? as follows:

Here, x is the sparse representation of signal m in the basis defined by ?.
Dynamic images have much higher sparsity than static images because of the presence of significant temporal correlations associated with periodic motion or gradual evolution. Therefore, a dynamic image series can have sparse representation with an appropriate transform applied along the dynamic dimension. Fig. 2.4 shows an example of sparse representation of a cardiac cine image series, in which a temporal FFT is employed as the sparsifying transform.

Fig. 2.4. A cardiac cine image series has temporal correlation because dynamic region is limited in only a small region, while the background is static. An FFT can be employed along the temporal dimension to sparsify the dataset.
Reference
1. Purcell EM, Torrey HC, Pound RV. Resonance Absorption by Nuclear Magnetic Moments in a Solid. Phys Rev 1946;69(1-2):37-38.
2. Bloch F. The Principle of Nuclear Induction. Science 1953;118(3068):425-430.
3. Macovski A. Noise in MRI. Magn Reson Med 1996;36(3):494-497.
4. J; C, Est A. Reducing MR imaging time by one-sided reconstruction. Magn Reson Imaging 1987;5:526.
5. Noll DC, Nishimura DG, Macovski A. Homodyne detection in magnetic resonance imaging. IEEE Trans Med Imaging 1991;10(2):154-163.
6. Amartur S, Liang ZP, Boada F, Haacke EM. Phase-constrained data extrapolation method for reduction of truncation artifacts. J Magn Reson Imaging 1991;1(6):721-724.
7. Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med 1997;38(4):591-603.
8. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999;42(5):952- 962.
9. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47(6):1202-1210.
10. Sodickson DK, McKenzie CA. A generalized approach to parallel magnetic resonance imaging. Med Phys 2001;28(8):1629-1643.
11. Schönberg SO, Dietrich O, Reiser MF. Parallel Imaging in Clinical MR Applications. Med Radiol Diagn Ima 2007:1-564.
12. Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM. SMASH, SENSE, PILS, GRAPPA: how to choose the optimal method. Topics in magnetic resonance imaging : TMRI 2004;15(4):223-236.
13. Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J Magn Reson Imaging 2012;36(1):55-72.
14. Larkman DJ, Nunes RG. Parallel magnetic resonance imaging. Phys Med Biol 2007;52(7):R15- 55.
15. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med 2010;64(2):457-471.
16. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med 2000;43(5):682-690.
17. Candes E, Romberg J, T. T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory 2006;52:489-509.
18. Donoho D. Compressed sensing. IEEE Trans Inf Theory 2006;52:1289-1306.
19. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58(6):1182-1195.
20. Liang D, Liu B, Wang J, Ying L. Accelerating SENSE using compressed sensing. Magn Reson Med 2009;62(6):1574-1584.
21. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med 2010;64(3):767-776