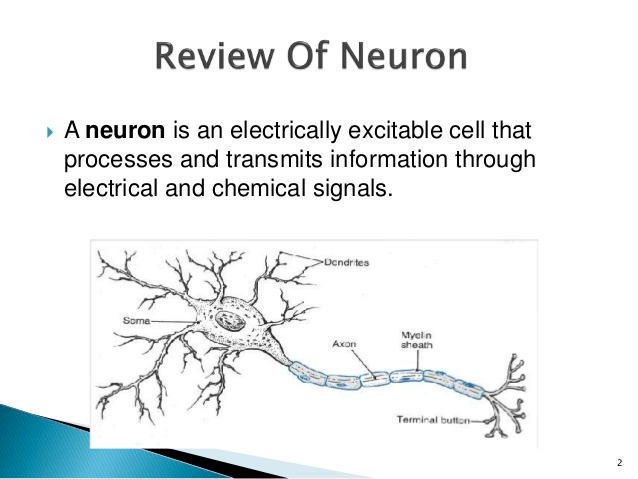
Neuron Model
The brain is a network of billions of neurons , which makes the brain orders of magnitude more dense than state-of-the-art silicon-based VLSI electronic systems and thus challenging to map and study with conventional methods . Furthermore, it is estimated that the human brain can process, analyze, and learn with a power consumption of as low as 10 W . As a result, biologically inspired computing systems, commonly referred to as neuromorphic systems, have gained increasing popularity not only due to their lower power requirements relative to traditional systems, but also due to their potential to perform tasks that traditional systems cannot achieve, including a variety of complex recognition and classification problems .In theoretical neuroscience, a common approach to study brain activity is to employ the recordings of electrical activity in the extracellular medium, where the electric currents from active processes superimpose and generate a potential difference with respect to a fixed reference potential . The electrode tip of a Micro-Electrode Array (MEA) can capture the electrical field changes generated by the voltage differences in the medium. The recording amplitude scales are inversely proportional to the distance between the source (neuron) and the recording site . These tips or channels can be strategically placed intracortically to record neuronal activity with sub-millisecond precision, and the recordings will contain characteristic action potential waveforms, commonly referred to as spikes in the 500-3k Hz frequency band . Another approach to study the brain and develop systems which could potentially exploit its yet-to-be-understood computational agility has focused on building artificial network models of neurons. The artificial models would mimic relevant properties of individual components or systems under study. In particular, building a network model requires selecting the characteristics that will describe the components of the model, ranging from the activity of individual neurons to more complex elements along the system hierarchy.
Spiking Model
Among all the sources of variability in extracellular recordings, three basic points can be taken into consideration when developing extracellular recording models to test spike detection and sorting algorithms: the source of firing activity, extracellular noise, and waveform variability. In general, the simplest approach to model neural activity recorded from the extracellular medium would be to add Gaussian noise to action potential waveforms extracted from extracellular recordings. However, this approach fails to reproduce real recording features such as possible spectral similarity between noise and spikes which can greatly affect the shape of spike waveforms. In another approach , a database containing previously recorded spike waveforms is employed to generate a model by placing waveforms at random times where single-unit activity is simulated to have an amplitude as a constant multiple of the level of the detection threshold. This model also includes realistic background noise including a superimposition of spike waveforms with amplitudes inversely proportional to their distance from the electrode tip. However, this model lacks adequate representation of waveform variability in individual profiles at the fixed detection threshold levels, and does not present a realistic source of noise, since it does not lead to a characteristic 1/f spectrum. In , a compartmental model was developed to simulate neuronal activity near a recording electrode in addition to including spikes waveforms to generate background noise. However, this model also does not consider waveform variability and is rather restricted in terms of firing variability. In , a model was generated through visual inspection from a dataset and noise was produced from segments without spikes from the original recordings; however, this model also does not fully characterize waveform variability or firing variability in terms of rate or interspike intervals. More detailed approaches such as , where extracellular potentials are calculated from biophysical models, are not only more computationally intensive, but can also make it more difficult to understand where or why an applied method can fail. This work is underpinned by two major aims: to find parametric characteristics to describe a set of visually inspected recordings by modeling the neurons present in the recorded segments with commonly employed distributions, and to employ these characteristics to generate and validate a flexible extracellular model to be used as an evaluation framework for spike detection algorithms. The developed models presented a variety of firing and timing characteristics as well as rich waveform variability and noise with similar spectral characteristics as noise extracted from real recordings, and thus address the shortcomings of similar methods as discussed previously.
Spike Detection
There are several detection algorithms that have been developed specifically for spike detection in extracellular recordings. In high SNR (≥ 5 dB) settings, a voltage threshold can be used as a spike detection method. In this case, every point in the recording where the voltage exceeds the threshold is collected as a timestamp. However, simple threshold algorithms are highly susceptible to SNR, and are thus not ideal for in vivo recordings, where increased activity, additional noise level and movement artifacts are typical. Conversely, computationally intensive algorithms are optimal for longitudinal offline studies but not convenient for in vivo or closed loop experiments given their high data transfer requirements for transmission and processing loads. Furthermore, most spike detection algorithms have been validated on models with high SNR, with almost uniform neuronal profiles, and without the experimental artifacts present in online in vivo recordings.To address these deficiencies, the models including parametrized characteristics of real extracellular recordings introduced in the first section were employed to compare typically employed spike detection algorithms. These models present a more challenging environment as characteristics such as variability of spike profiles, number of individual spiking units, singleunit firing rate, and SNRs are included. The present work is underpinned by two major objectives: to propose an adapted spike detection algorithm based on known biophysical characteristics of action potentials, and to test and compare the performance of the proposed detection mechanism with other commonly employed methods. The adapted version of the detection algorithm originally developed for in vitro cortical recordings leads to improved efficiency and performance calculated via receiver operating characteristics (ROC) curves across different realistic SNR conditions, thus demonstrating to have features compatible with the use for online in vivo applications.
MEA Recording integrity and variability
There is a demand for ever-increasing chronic electrode channel counts for neural recordings to enable a greater understanding of brain dynamics in vivo. The electrodes typically employed for extracellular recording consist of rigid substrates, which can induce a response within the brain tissue to encapsulate invasive foreign elements, causing individual or multiple channels to become compromised or unusable . At the beginning of an electrophysiological experiment setup, the recording quality is usually visually inspected by the user. A practical challenge in electrophysiological recordings is identifying viable, non-functional, and shortcircuited channel locations. As channel counts increase, it becomes unwieldy to manually assess the quality of neural recordings and subsequently detect and characterize neural activity across electrodes. This necessitates a way to quickly validate and quantify the reliability of available extracellular signals on which to perform spike detection and sorting. Assurance of accurate and reliable recorded data becomes essential in closed-loop architectures such as efferent decoders, where the neuronal activity is decoded to obtain movement-related information, or in spike-triggered experiments, where individual neuron activity is employed to trigger stimulation pulses. There is evidence that the variations in the recordings due to the mechanical mismatch between electrode array and brain tissue can affect the performance of decoders , and in intracortical microstimulation (ICMS) experiments, some of these variations may even be exacerbated . In addition, in current spike-triggered paradigms, a trigger neuron is chosen through visual inspection and may be subject to experiment-to-experiment variability through bias. Accordingly, the objectives of this work have been to determine an approach to assess signal quality of extracellular recordings to perform accurate spike identification and to promote unbiased selection of reference neurons through online evaluation of single-unit activity. This process facilitates a rapid assessment of signal quality and the unbiased selection of trigger neurons by matching reference neurons across a series of experiments previously visually selected by experimenters. Automation of these processes should optimize similar experiments and increase experimental reproducibility.
Non-Linear Time Delay Line
Among neuromorphic systems, reservoir computing systems have gained particular attention due to their simplified approached to solve complex tasks . The traditional reservoir architecture employs three different layers: the input layer, the reservoir and the output layer. The input layer feeds the input signals to the reservoir via fixed randomly-weighted connections to nodes in the reservoir. The reservoir layer consists of randomly connected nonlinear nodes that can form a feedforward or recurrent neural network. The output layers match the states of the reservoir with the desired output signal through an output weight matrix that can be trained online or offline. A lower-dimensional reservoir, the time delayed feedback reservoir,substitutes the classic reservoir network with randomly connected neurons or nodes with a single nonlinear node subject to a delayed feedback. This simplification has shown to achieve comparable performance with respect to more traditional approaches, thus highlighting the inherent capabilities of temporal processing in nonlinear systems.