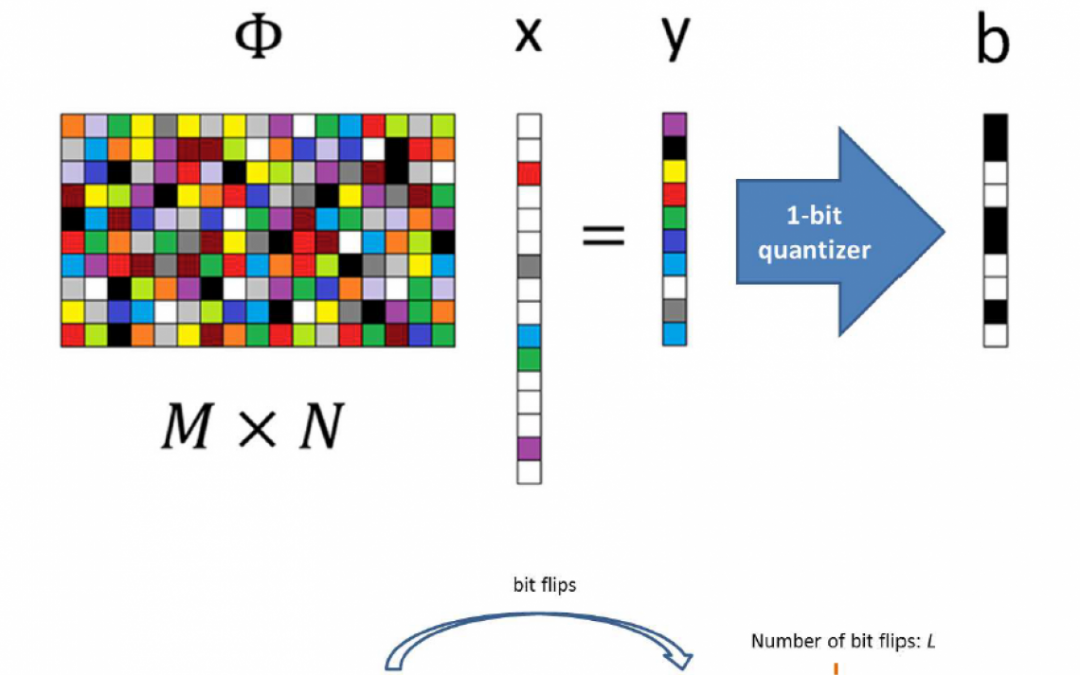
Compressive Sensing
Traditionally, in order to increase the resolution of a sensor, one had to increase the number of measurements. This means that the SWAP-C must also increase. A camera with just a few megapixels FPA costs less than one with hundreds of megapixels. The cost of designing the optics will also need to scale to provide enough optical resolution. In a perfect world, one could capture all the information one needs from just a few measurements.With a discrete signal one needs at least as many measurements as there are signal elements to solve the inverse problem. If the number of measurements is fewer, then the inverse problem is under determined. Conventional signal processing dictates that accurate reconstruction of the signal-of-interest is highly improbable Fortunately, a signal acquisition technique called compressive sensing allows one to design sensors that solve these types of highly under determined inverse problems. As discussed earlier, much of the data being generated by sensors are redundant. Images, spectra, video, and audio data of real-world signals tend to exhibit patterns or redundancies that can be exploited. This allows a compression algorithm to signicantly reduce the amount of data needed to represent the signal. There is a class of compression algorithms called lossy . In lossy compression, not only are redundancies exploited but data that is deemed insignicant to the signal quality is discarded. Only the most important part of the signal is kept as part of the compressed representation of the original signal. When the signal is uncompressed, the amount of data is less than the original measured data. The difference in quality is often unnoticeable to a human observer. In both lossless and lossy compression, the goal is to obtain a sparse representation of the signal. A sparse representation means that the signal can be well approximated with only a few non-zero elements in a representation basis. A representation basis is a basis in which the signal-of-interest is sparse. For example, most natural images are sparse in the Fourier basis. The representation basis is typically not the native basis of the signal-of-interest, i.e. pixel number or spectral channel. Researchers pointed out that traditional sensors tend to produce vast amounts of measurement data, but often the majority of data is redundant and discarded in the compression step . This led to the idea that sensors can be designed to directly measure the most relavent data in a signal, suggesting a measurement scheme that can measure a compressed form of the signal. This is the idea behind compressive sensing sometimes known as compressive sampling. If the measurements are compressive then it should be possible to signicantly reduce the number of measurements to accurately reconstruct the signal. Note that there is a distinction between compressive sensing and the traditional approach of sensing and then compressing. In the traditional approach, compression algorithms operate as a post-processing step. Therefore, a traditional compression algorithm will have access to the entire signal to look for redundancies and convert it into a sparse representation. In compressive sensing, one attempts the compression directly and therefore do not have access to the entire uncompressed signal. The algorithms must assume that the signal has a sparse representation. The question of how to actually measure or code the analog signal to directly obtain compressed data is also important. Fortunately, random coding tends to work well in many instances when the signal has a sparse representation. However in many cases, designed codes can signicantly outperform random coding. I will discuss other types of coding schemes that can be used to outperform random codes. The idea of compressive sensing seems to be similar to the concept of multiplex sensing. However, there is an important distinction to be made. In compressive sensing, the aim is to obtain the relavent information in as few measurements as possible. In multiplexing, the goal is to overcome limitations mainly due to lack of SNR. Many compressive sensing schemes also employ multiplexing. One useful example of compressive sensing versus traditional sensing is the single pixel camera. The single pixel camera is a multiplexing camera architecture that uses time sequential random measurements and recovers the image in signicantly fewer measurements (equal to number of exposures pixels) than the conventional camera, see Figure 6. Another example is the Coded Aperture Snapshot Spectral Imaging (CASSI) architecture, which can reconstruct a spectral data cube in signicantly fewer FPA exposures than a traditional spectral imaging architecture. Another important distinction is between reconstruction and task-specic sensing. Task-specic sensing tends to refer to measurement techniques that attempt to directly perform tasks such as detection, classication, and estimation without the intermediate step of reconstructing the high-dimensional signal. Compressive sensing is useful not just of overcoming resolution limitations in reconstruction but for task-specic sensing. For example, in facial recognition the goal is detection of an individual person. Reconstruction of the face image is simply an intermediate step, therefore, one can develop a compressive sensing scheme that is optimal for direct facial detection, skipping the step of image reconstruction. Computational sensors can overcome classic engineering trade-offs in sensor design. However, there is a unique set of challenges related to computational sensing.
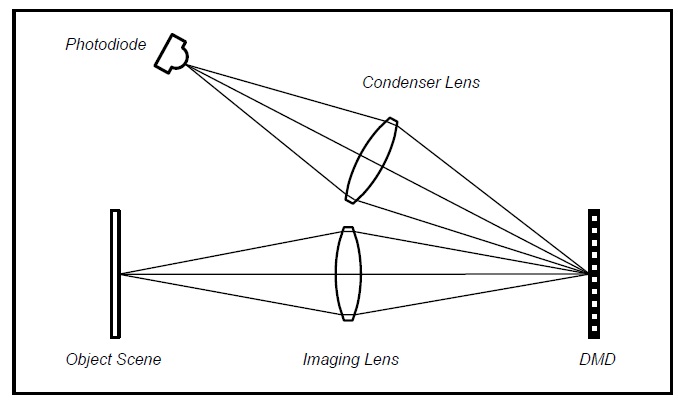
Figure 6 : A single pixel camera architecture. The object scene (or intermediate image) is imaged onto a Digital Micro-Mirror Display (DMD). The each micro-mirror of DMD re ects light towards the photodiode or to another direction. This acts as a point-by-point multiplication of the discrete image with the DMD pattern. The condenser lens sums any light reected by the DMD and focuses it onto the photodiode. This can be described mathematically as a vector multiplication of the image with the DMD pattern.