T1 Relaxation Thermometry
T1 relaxation refers to the recovery of the longitudinal magnetization. The physical process underpinning T1 recovery involves energy dissipation from the excited spins into the surrounding tissue lattice through interactions with the randomly fluctuating molecular dipoles. The addition of heat alters this energy exchange in a linear fashion over a range of relevant treatment temperatures. T1 imaging can therefore be employed to estimate temperature. Quantitative T1 sequences are too slow for the temporal resolution typically required in thermometry procedures and so faster sequences must be used. These include RF-spoiled gradient echo, inversion recovery, and single-shot fast spin echo sequences.
A benefit of this technique is that it can be used to monitor temperature in fat, as fat molecules produce a measureable T1 signal. This is in contrast to the subsequent two methods which are not sensitive to temperature changes in fat. Unfortunately T1 imaging of heating effects suffers from several major drawbacks. The linear dependence of temperature on T1 is not maintained once coagulation occurs, limiting the technique’s usefulness in ablative procedures. T1 values are tissue-specific, necessitating estimates of the T1 value for each target tissue to be imaged.
This is further complicated by the fact that most voxels contain a mixture of tissue types (e.g., muscle, tumour, blood), thus necessitating a pre-calibration step to determine per-voxel T1 estimates. The fast sequences used necessarily suffer from reduced SNR; and the PRF shift effect causes phase dispersal independent of T1 leading to an additional marked loss of SNR beyond that inherent to the sequence. Finally, T1 contrast diminishes with higher field strength limiting the technique’s usefulness to lower field strength magnets.
Water diffusion thermometry
MRI can be used to produce diffusion-weighted images (DWI) of water molecules; that is, images that indicate the relative mobility of water in tissue. This is accomplished by playing out a set of bipolar gradients. Spins that remain unchanged in location will be re-phased while those that move (primarily due to thermal Brownian motion) will not be completely re-phased, resulting in a detectable loss of signal. The amount of signal attenuation is related to the sequence parameters as well as a physical constant known at the diffusion coefficient, D [/s]. The temperature may be computed from knowledge of the diffusion coefficient via thefollowing equation:

8
 and
and  are the initial temperature and diffusion coefficient values before heating occurs, and Ea represents the activation energy. This method is very sensitive (ΔD/ΔT ≈ 2%/°C) but suffers from several practical limitations. Typically a value of Ea = 0.2 is used for temperature calculations, based on the activation energy of water [36]. In fact, Ea exhibits a linear variation over a roughly 30°C temperature range; however, the slope is relatively flat and treated as a constant. Additionally Ea does vary with tissue type.
are the initial temperature and diffusion coefficient values before heating occurs, and Ea represents the activation energy. This method is very sensitive (ΔD/ΔT ≈ 2%/°C) but suffers from several practical limitations. Typically a value of Ea = 0.2 is used for temperature calculations, based on the activation energy of water [36]. In fact, Ea exhibits a linear variation over a roughly 30°C temperature range; however, the slope is relatively flat and treated as a constant. Additionally Ea does vary with tissue type.

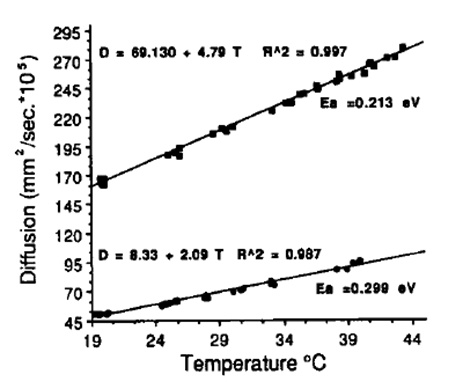
Figure 3. Diffusion versus temperature relations for two different
gel phantoms. The activation energies for these two phantoms
are 0.213 and 0.299 eV
Figure 3 shows the relationship between the diffusion coefficient and temperature elevation, and the effect of differing tissue types. Another complication is that the mobility of water depends on the structure of the barriers in the local environment: cell walls, proteins, and membranes. Because of this the value of D can be influenced by physiological changes that alter these barrier structures. This includes tissue coagulation and edema (swelling), which can alter cell size. Membrane permeability is also affected by temperature thus introducing a non-linear relationship between the value of D and the temperature. Another problem is that the water mobility may exhibit a directional dependence. To fully capture the diffusion behaviour an estimate of D would be needed for all three spatial dimensions. This adds significant time to the scan. DWI is also quite sensitive to motion. With water mobility on the order of 10um, even slight motion can cause inaccurate estimations. Finally, relatively long TEs are required in order to sensitize the spins to diffusion (longer TEs allow greater spin displacement to take place). This has the undesirable effect of increasing the phase dispersal that occurs due to PRFS, enhancing the signal loss. Signal loss from the PRFS effect cannot be distinguished from diffusion effects, leading to artefacts and/or incorrect diffusion estimates.