Signal Model and Problem Statement
In this post, we talk about Signal Model and Problem Statement.
The Nyquist bandwidth is denoted by W and it is composed of K disjoint. sub-bands representing the PU’s. The bandwidth of each sub-band is upper bounded by B Hz and their locations in F are unknown to the SUs. The ith sub-band signals is given by
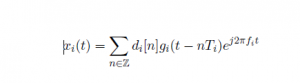
where di[n] is a sequence of modulation symbols, gi(t) is a pulse shaping function, and fi is the carrier frequency. Then the observed signal at each SU is,

where n(t) is complex additive white Gaussian noise (AWGN) with noise power 2 and it is assumed that each sub-band signal is independent with zero mean.This research defines the following spectrum sensing problem: Given a desired bandwidth to sense W,identify all active frequency bands that compose the K sub-band signals in F.Since the locations of each sub-band signal are unknown, the problem becomes that of blind multi-band spectrum sensing.In order to reliably sense and detect the presence (or absence) of a PU in a wideband spectrum, several technical challenges must be overcome first. In WSS, W typically spans several GHz which requires analog-to-digital converters (ADC) operating at several Giga samples per second. Unfortunately,ADC’s operating at these rates suffer from high power consumption, low bit resolution, and high costs .Furthermore, factors such as multi-path fading and shadowing will affect the detection performance of any CR. Popular approaches for mitigating these technical challenges include cooperative wideband spectrum sensing(CWSS) and sub-Nqyuist sampling. In the following sections, two common approaches to wideband sub-Nqyuist spectrum sensing are reviewed. This includes compressed sensing (CS) and multi-coset (MC) Sampling.

