Session 05: Creating Arrays in MATLAB

MATLAB stands MATrix LABratory means Lab matrix well. The reason for this naming is that all MATLAB variables are arrays. That is, each variable can contain several elements. By array in MATLAB, we mean the same vector and matrix in MATLAB that you have definitely seen in mathematics. One of the most important parts of MATLAB is working with vectors and matrices in MATLAB. So familiarity with how to define and work with arrays in MATLAB is very important. The table of contents of this fourth session of free MATLAB training includes:

Vector definition in MATLAB

One-dimensional arrays are called vectors. We have two types of vectors in MATLAB: row vector and column vector. A row vector has one row and several columns (image below, top row). In contrast, a column vector has multiple rows and a column (image below, bottom row). They use a m × n symbol to indicate the dimensions of the arrays. In this symbol, m represents the number of rows and n the number of columns. With this description, the line vector of an array with dimensions l 1 × n is the column vector of an array with dimensions m × 1. Next, in two separate sections, we define a line vector in MATLAB and a column vector in MATLAB.

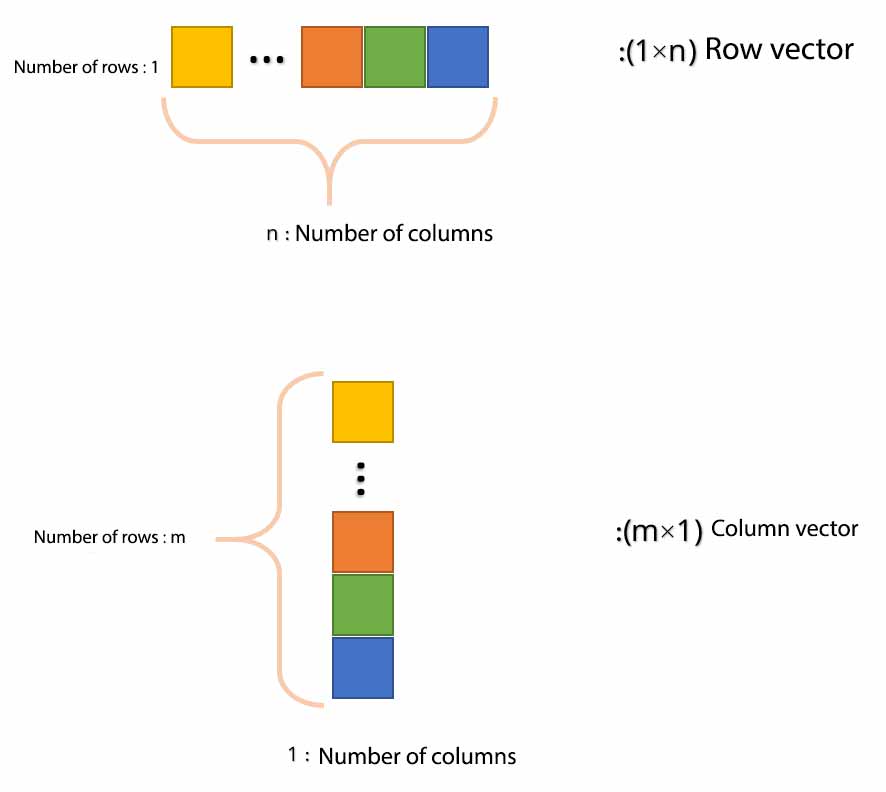
vectors matlab

1- Line vector in MATLAB

In MATLAB, you can create a vector using the bracket ([]). To define a vector in MATLAB, you can write vector elements in brackets. By elements, we mean the same numbers inside the vector. Then separate these elements with space (comma) or comma (,) . For example, we want to create a variable called x that is a row vector with elements 3 and 5. In this case, we must write:

>> x = [3 5] 
x = 
     3 5

MATLAB removed the bracket itself in the show, which does not matter. Now we separate the numbers inside the bracket with a comma:

>> x = [3, 5] 
x = 
     3 5

As you can see, the result is the same as before. That is, whether you use a space to define a vector or a comma, the result does not change. You are free to work with any sign you are comfortable with. Well, let’s go to the first exercise of the array session in MATLAB Do not forget, solve it yourself and then see the answer… Exercise 1: Create a line vector called x with two elements 7 and 9.

>> x1 = [7, 9] 

x1 = 
     7 9

>> y = [1; 3] 

y =     1     3

>> y = [1
3]
y =
    1
    3

>> y = [1  3] 

y = 1 3

>> [6 * 3 pi / 2]
ans =

18.0000 1.5708

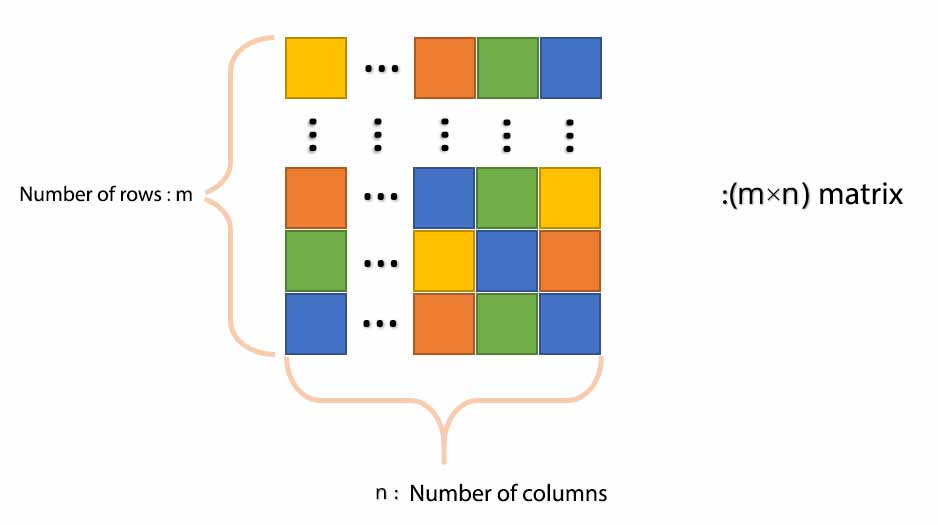
In the previous section, we learned how to define row and column vectors. In the last part of the array session in MATLAB, we want to learn the definition of a matrix together. Two semicolons and; They gave us the ability to create rows and columns. Now we can make a matrix from the combination of these. To create a matrix, we combine spaces and semicolons to create an array with several rows and columns. Two-dimensional arrays in a MATLAB are called matrices. Note that priority is given to rows, and for example, if we want to create a 3 × 2 matrix, we must define our matrix line by line. We have already learned that when we say that an array is m × n, that is, m has rows and n columns. That is, here we want to define a matrix that has 2 rows and 3 columns. Note how to define the following matrix:

>> x = [3 4 5; 6 7 8]
x =
3 4 5
6 7 8

Again, in the example above, we first defined the first line (ie, 5, 4, 3). Next with; Go to the next row and then enter the second row (ie 8 7 6). Now let’s define the above matrix in another way:

>> x = [4 5 6
        7 8 9]
x =
4 5 6
7 8 9

Defining a matrix in this way is probably much clearer to you. MATLAB is not particularly strict in defining matrices and vectors. So you can define an array with any of the methods mentioned that you are more comfortable with.

Note each element of the array in MATLAB (both vector and matrix), elements are known.

Note The objects of a matrix, like a vector, can be the result of an algebraic operation or the output of a function.

Exercise 6: Create a matrix called x_y with dimensions of 3 × 2 with arbitrary values.

x = [7 9]
x = [7,9]
x = [7 , 9]
x = [7, 9]