Cellular respiration and oxygen transport in the body
A basic understanding of cellular respiration is crucial to this work; to wit, a brief overview will be provided. There are two types of cellular respiration in the body: aerobic and anaerobic respiration. Aerobic respiration requires oxygen and glucose, while anaerobic respiration requires only glucose . Both reactions produce adenosine triphosphate, and while aerobic respiration is more ecient, anaerobic respiration produces energy more quickly. The dierent characteristics of aerobic and anaerobic metabolism produce dierent muscle phenotypes based on the dominant method of glucose utilization in that particular ber type: aerobic metabolism produces smoothtwitch bers and steady muscle movements, while anaerobic metabolism produces fast-twitch bers and re ex movements. Both phenotypes of muscle ber are utilized during exercise, but slow-twitch bers relying on aerobic metabolism are predominantly used during moderate exercise in healthy individuals.
Since aerobic metabolism utilizes oxygen for energy production, a brief review of oxygen-based metabolism is helpful for a better understanding of our study.Oxygen ( ) is transported through the body by hemoglobin, an iron-rich metalloprotein found in red blood cells. Hemoglobin exists in two forms: deoxygenated, also referred to simply as hemoglobin (Hb), and oxygenated, generally referred to as oxyhemoglobin (
) is transported through the body by hemoglobin, an iron-rich metalloprotein found in red blood cells. Hemoglobin exists in two forms: deoxygenated, also referred to simply as hemoglobin (Hb), and oxygenated, generally referred to as oxyhemoglobin ( ). As red blood cells move through the body and pass through capillaries, cells utilizing aerobic respiration absorb the
). As red blood cells move through the body and pass through capillaries, cells utilizing aerobic respiration absorb the  from
from  , converting
, converting  into Hb. The blood is then recirculated to the pulmonary system where Hb binds with
into Hb. The blood is then recirculated to the pulmonary system where Hb binds with  during the respiration cycle, and the process begins again.
during the respiration cycle, and the process begins again.
Tissue Optics
A tissue oximeter uses continuous-wave light at multiple wavelengths to determine the relative changes in tissue oxygenation and blood volume via absorption spectroscopy. In the most generic form of muscle oximetry, a source emits light which penetrates the tissue and is scattered back to a detector at the plane of incidence. The dierence in the input intensity and the intensity of light measured by the detector can be used to reconstruct the composition of the material. An understanding of light-tissue interaction is key to understanding of this work, and is presented here. Biological tissues such as skin and muscle are non-homogeneous, turbid, anisotropic, and strongly scattering. For a fully rigorous mathematical treatment of continuous wave monochromatic light propagation in tissue, one must solve the radiation transfer equation,

figure 1
where I(r , s) is the radiance,  is the eective molar extinction coecient,
is the eective molar extinction coecient,  is the eective scattering coecient, p(s,
is the eective scattering coecient, p(s,  ) is the scattering phase function, and
) is the scattering phase function, and is the unit solid angle about
is the unit solid angle about  . Appropriate boundary conditions would need to be found for each layer of tissue; the epidermis has dierent optical properties than the dermis, for instance. As can be seen from Figure 1, even using a simplied rendition of the layers of tissue between the surface of the skin and the skeletal muscle would leave us with four coupled dierential equations to solve. Fortunately, we are able to apply diusion theory to simplify this problem. Di usion theory can be utilized when the absorption coecient,
. Appropriate boundary conditions would need to be found for each layer of tissue; the epidermis has dierent optical properties than the dermis, for instance. As can be seen from Figure 1, even using a simplied rendition of the layers of tissue between the surface of the skin and the skeletal muscle would leave us with four coupled dierential equations to solve. Fortunately, we are able to apply diusion theory to simplify this problem. Di usion theory can be utilized when the absorption coecient,  , of the tissue is much less than the reduced scattering coecient,
, of the tissue is much less than the reduced scattering coecient, , which is related to the anisotropy factor of the tissue. Both skin and muscle satisfy this condition, and diusion
, which is related to the anisotropy factor of the tissue. Both skin and muscle satisfy this condition, and diusion
![A broad sketch of the layers of skin on top of skeletal muscles [29]. Each of these layers has different optical properties.](https://matlab1.com/wp-content/plugins/wp-fastest-cache-premium/pro/images/blank.gif)
A broad sketch of the layers of skin on top of skeletal muscles [29]. Each
of these layers has different optical properties.

2
where  is the intensity of the source at wavelength
is the intensity of the source at wavelength  , I is the intensity of light measured by the detectors at some time t, L is the optical path length discussed below,
, I is the intensity of light measured by the detectors at some time t, L is the optical path length discussed below,  is the molar extinction coecient of the
is the molar extinction coecient of the  component of the tissue, and
component of the tissue, and  is the concentration, or \weight”, of the
is the concentration, or \weight”, of the  component in the tissue. The absorption coecient of the
component in the tissue. The absorption coecient of the  component of the tissue is given by
component of the tissue is given by  . The exact molecular composition and optical properties of a given in vivo tissue will change from sample to sample – average values acquired from tables are used instead. The quantity
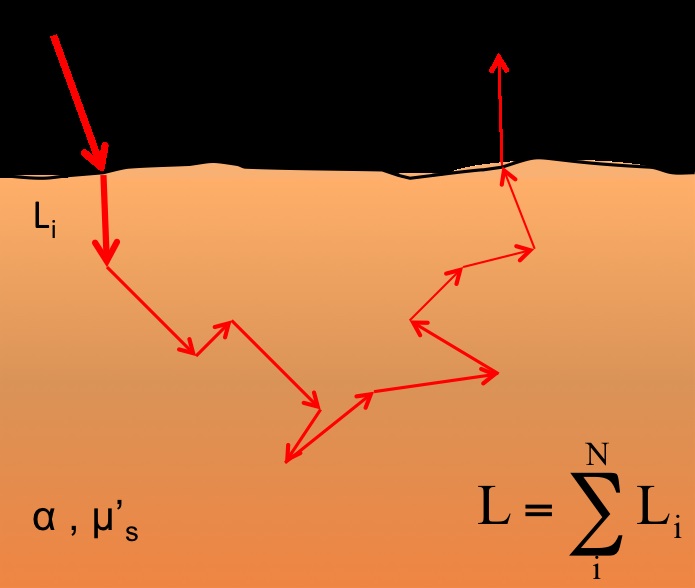
. The exact molecular composition and optical properties of a given in vivo tissue will change from sample to sample – average values acquired from tables are used instead. The quantity  is often referred to as attenuation (A); all future equations will be presented in this manner. When light is scattered, the photons undergo a random walk phenomenon, as shown in Figure 2 – each photon travels along a dierent path between the source and detector. For photons that are scattered back to the plane of incidence, the total path is \banana-shaped” overall and is longer than the distance between the source and detector. The optical path length is dened as the average of these paths; i.e.,
is often referred to as attenuation (A); all future equations will be presented in this manner. When light is scattered, the photons undergo a random walk phenomenon, as shown in Figure 2 – each photon travels along a dierent path between the source and detector. For photons that are scattered back to the plane of incidence, the total path is \banana-shaped” overall and is longer than the distance between the source and detector. The optical path length is dened as the average of these paths; i.e.,

The random walk phenomenon in 2 dimensions. Light entering the tissue
(I0) is multiply scattered inside the tissue before exiting at the plane of incidence.
The total path length (L) is longer than the distance between the source and detector
the average distance that a photon travels through the given medium before reaching the detector. The optical path length changes depending on the distance between the source and detector and the optical properties of the material, which vary with wavelength. This relationship is shown in Eqn. 3 (below), where  is the sourcedetector distance, and
is the sourcedetector distance, and  and
and  are the absorption and reduced scattering coecients of the material, respectively
are the absorption and reduced scattering coecients of the material, respectively

3
In the case of non-homogeneous anisotropic media, such as skin and muscle (Figure 1), the diusion equations become a bit more complicated. In muscle oximetry, we are only interested in a change in concentration of two molecules, Hb and  , over time. As a result, we can eliminate from consideration any components of the tissue that will not change over time, simplifying Eqn.2. Following previous work, we assume that the optical properties of the epidermis, dermis, and hypodermis will not change signicantly over time. This is a reasonable, given the relatively short timescale of oximetry experiments. By making this assumption, we have entirely eliminated skin and fat from consideration; the only layer we need to model is the layer of muscle. Muscle tissue can be treated as though it is composed entirely of Hb and
, over time. As a result, we can eliminate from consideration any components of the tissue that will not change over time, simplifying Eqn.2. Following previous work, we assume that the optical properties of the epidermis, dermis, and hypodermis will not change signicantly over time. This is a reasonable, given the relatively short timescale of oximetry experiments. By making this assumption, we have entirely eliminated skin and fat from consideration; the only layer we need to model is the layer of muscle. Muscle tissue can be treated as though it is composed entirely of Hb and  . This approximation is justied: myoglobin, the main protein in muscle bers, while present in both its oxygen-bound and reduced forms, is very nearly indistinguishable from hemoglobin optically and has a lower concentration than hemoglobin in muscle and therefore is not treated separately in the calculations. The modied Beer-Lambert law can now be expressed as
. This approximation is justied: myoglobin, the main protein in muscle bers, while present in both its oxygen-bound and reduced forms, is very nearly indistinguishable from hemoglobin optically and has a lower concentration than hemoglobin in muscle and therefore is not treated separately in the calculations. The modied Beer-Lambert law can now be expressed as

4
where  refers to a change in attenuation,
refers to a change in attenuation,  is the baseline intensity of light at a wavelength
is the baseline intensity of light at a wavelength  ,
,  is the intensity of light measured at some time t,
is the intensity of light measured at some time t,  is the optical path length, and
is the optical path length, and  and
and  and
and  and
and  are the change in concentration over time and molar extinction coecients of Hb and
are the change in concentration over time and molar extinction coecients of Hb and  , respectively. We will solve this equation at two wavelengths to nd
, respectively. We will solve this equation at two wavelengths to nd  and
and  . Although Eqn. 1.4 is wavelength dependent, thus far we have not discussed how our choice of wavelengths aects the calculations. Figure 1.3 shows a plot of the molar extinction coeents of Hb and
. Although Eqn. 1.4 is wavelength dependent, thus far we have not discussed how our choice of wavelengths aects the calculations. Figure 1.3 shows a plot of the molar extinction coeents of Hb and  ; the orange box indicates the NIR range. Since
; the orange box indicates the NIR range. Since  , the absorption coecient, we expect low absorption in the NIR range. This results in both an increased depth of penetration and a larger signal. Because of these optical properties, the NIR range has been termed the “diagnostic window” for oximetry. For our oximeter, we have chosen to use
, the absorption coecient, we expect low absorption in the NIR range. This results in both an increased depth of penetration and a larger signal. Because of these optical properties, the NIR range has been termed the “diagnostic window” for oximetry. For our oximeter, we have chosen to use  = 735 nm and
= 735 nm and  = 850 nm to solve for
= 850 nm to solve for  and
and  . More details are given in Section 2.i Once we have solved Eqn. 4 for
. More details are given in Section 2.i Once we have solved Eqn. 4 for  and
and  , we can nally solve for the
, we can nally solve for the
![The molar extinction coecients of Hb (blue) and HbO2 (red) [30]. The orange box highlights the NIR range. Since the molar extinction coecients are much smaller in the NIR range than elsewhere in the spectrum, we expect Hb and HbO2 to absorb less light at these wavelengths. The NIR range has been termed the \diagnostic window" for oximetry.](https://matlab1.com/wp-content/plugins/wp-fastest-cache-premium/pro/images/blank.gif)
The molar extinction coecients of Hb (blue) and  (red). The orange box highlights the NIR range. Since the molar extinction coecients are much smaller in the NIR range than elsewhere in the spectrum, we expect Hb and
(red). The orange box highlights the NIR range. Since the molar extinction coecients are much smaller in the NIR range than elsewhere in the spectrum, we expect Hb and to absorb less light at these wavelengths. The NIR range has been termed the”diagnostic window” for oximetry.
to absorb less light at these wavelengths. The NIR range has been termed the”diagnostic window” for oximetry.
 ) and blood volume (
) and blood volume ( ) of the muscle using
) of the muscle using

5,6