K-space
The main purpose of k-space is to maintain the data acquired during a scan prior to processing the image. In the clinical world, k-space is one level in the creation of the image. It is not seen or stored in regular scans. In the research world often you have a choice in keeping the k-pace, for later processing, or changing the parameters in which it is acquired. Creating an MRI image requires the collection of acquired data. Each acquisition within a new transverse magnetization is created and sampled in k-space in a particular order. K-space is a two or three dimensional entity where there exist phase encoding directions along y or z and a frequency encoded direction along x. Changes to the acquisition method are possible and will be discussed later. These changes can affect the scanning and acquisition time, although potentially leading to artifacts. MRI acquires an image by selecting three different gradients, dedicated to spatial encoding, phase encoding, and frequency encoding.
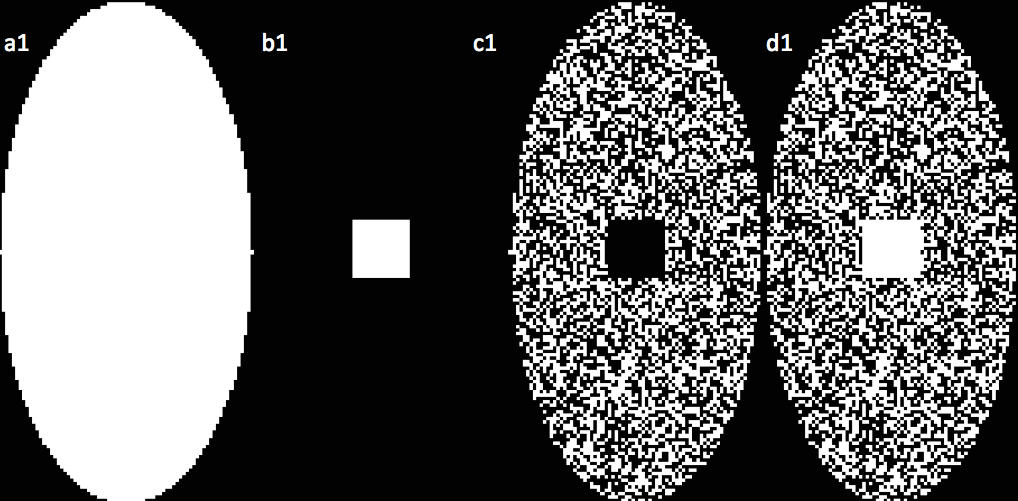

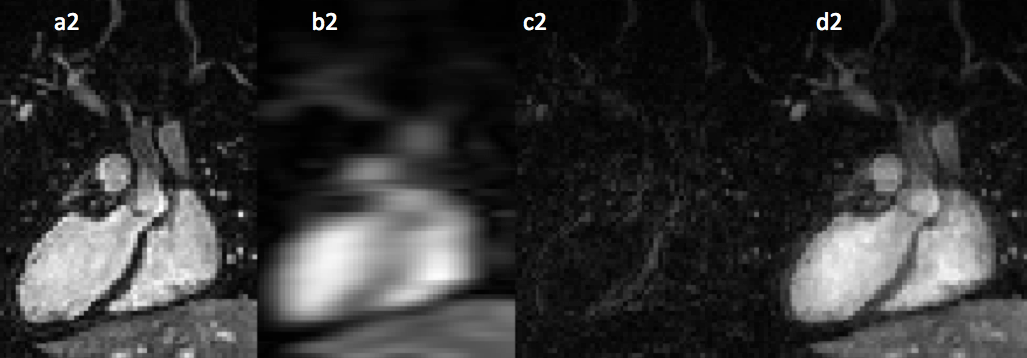
Figure 2: Image resolution is determined by the extent of the k-space that is covered. Top row represents the pattern chosen for image reconstruction (a1,b1,c1,d1): a1 represents the fully sampled k-space which is standard throughout all Phillips machine; a2 is the achieved cardiac image when the corresponding k5 space is reconstructed; b1 represents the k-space that is only sampled in the center; b2 is the reconstructed image and it can be seen that the center is extremely important in the contrast of the images; c1 represents the peripheral portion of the k-space sampled, as seen in c2 the peripheral of k-space contributes to the resolution of the image; d1 represents the uniformly undersampled k-space data which will be later reconstructed with a reconstruction algorithm, the original reconstruction will be d2.

Figure 3: Various k-space acquisition from the a) linear b) echo planar imaging c) radial d) spiral; from e-h these are in 3D space, e) linear f) stack of radial g) radial h) stack of spiral (Lustig, 2008).
Figure 2 displays k-space sampling trajectories and actual undersampling pattern. As it can be seen, each value represents a portion of the image and selectively picking areas, for sample the middle, you would have a blurred image with lower resolution. As shown in 6 Figure2 undersampling the k-space would not have a significant effect on quality unless certain essential parts of k-space are undersampled. Altering the acquisitions of k-space will result in different images and artifacts,(Lustig,2008). Also there are different trajectories (Figure 3) that k-space can be sampled to decrease scanning time and avoid certain artifacts like aliasing where there will be a misrepresentation of frequency instead of the actual. One of the most important concepts of k-space is the how the center of k-space contributes to contrast while the edges contribute to resolution.