Graph Theory
In this post, we talk about Graph Theory.
If the interaction topology of a networked power grid is represented using a directed graph G = (V,E) with the set of nodes V = 1,2, . . . ,n and edges E ∈ V ×V, and the neighbors of an agent i are denoted by Ni = { j ∈ V : (i, j) ∈ E}, the graph Laplacian of the topology can be defined as follows
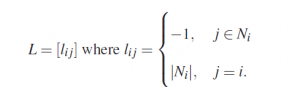
Here, |Ni| denotes the number of neighbors of node i (or the degree of node i).
the eigenvalues for the graph Laplacian of an undirected (n, k)-star graph are upper bounded by the Laplacian Spectrum λ∗ = 2deg(Sn,k) where deg is the degree of the certain topology. The following two definitions are derived
from the research that prove the stability and the consensus property of a graph topology with its graph Laplacian.
A local controller stabilizes the formation dynamics in a dynamic system topology if and only if it simultaneously stabilizes the set of N systems

where λi are the eigenvalues of graph Laplacian L.
If the eigenvalues of a specific system L22+1N−1 ·αT are λ2, . . . ,λN. Thus, there exists an invertible matrix T such that L22+1N−1 ·αT is similar to a Jordan canonical matrix

where Jk are upper triangular Jordan blocks, whose principal diagonal elements consist of λi. Therefore, T is an upper triangular block matrix, which together with the properties of Kronecker product, implies that the eigenvalues of L22+1N−1 ·αT are in the open left half plane.
The two definitions above are applied later to prove the consensus and stability of the proposed model. The Kronecker product of matrices A ∈ Rm×n and B ∈ Rp×q is defined as

which satisfies the following properties: