Fourier Transform
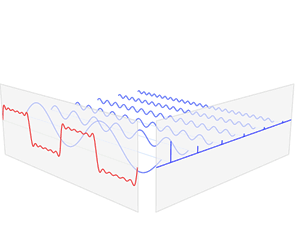
Fourier transform is an integral transform that in this case transforms a time function and expresses it as a function of frequency. An inverse Fourier transform represents the frequency function in time. The concept of Fourier transform becomes important in the study of complicated waves. Complex waves can be represented by the summation of simpler and basic waves such as cosine and sine functions. This is better viewed as an image, as shown in Figure 1. Of particular interest is the fact that in MRI there is frequency and phase encoded spatial information that are used to create an image by changing the phase and frequency along the gradients. These frequencies are then collected in k-space, which is inversely transformed into an image by the Fourier transform. Fourier Transforms: this is the equation for a Fourier transform. Fourier Series: In the Fourier series a wave like function is created by using combination of simple sine and cosine waves. Arguably the most beneficial aspect of a Fourier series is that it is possible to deconstruct a complex wave into a smaller series of sine and cosine waves. Finite summation:
, for integers N ≥ 1Fast-Fourier Transform: A way to compute discrete Fourier transform and its inverse. Let be a complex number, the Discrete Fourier transform is defined as:
Figure 1: Fourier Transform- A simple transform breaking a complex wave (shown
in red) into simpler sine waves (shown in blue) in relation to time. Time (red) is
transformed to frequency domain (blue).