Discrete Tomography
If the amount of available projection data is limited (e.g. with few-view tomography,a limited angular range or data truncation) the reconstruction problem is ill-posed and conventional algebraic reconstruction methods tend to find solutions that do not correspond to the measured object. It then makes sense to exploit prior knowledge about this object. Such prior knowledge can come in many forms.
- If only a limited number of pixels do not represent air, the image is said to
be sparse with respect to the pixel basis. Research in the field of compressed sensing has shown that sparse images can be reconstructed from a small number of measurements, provided that the measurements satisfy certain randomization properties .
- Structures often have a homogeneous density and are very large with respect
to the pixel size. In that case the gradient image is very sparse. Reconstruction
is then referred to as a total variation minimization problem [4].
- Noise statistics can be taken into account with Expectation Maximization
(EM) algorithms.
- If a scanned object contains known components such as screws or implants,
their shapes can be modelled into the reconstruction process using like lihoodbased methods.
- Attenuation values are by definition always positive.
- Scanned objects or parts of it are usually piecewise constant and homogeneous.
- The exact attenuation factor of the materials present in the object and thus also the exact grey level in the reconstructed image can be known in advance.In this chapter, an algorithm is considered that exploits the last two items of this list. Consider an object that consists of a single homogeneous material. Its reconstructed image should then ideally contain only two grey levels: one for the background and one for the object. Conventionally, this constraint is enforced posteriori to the reconstruction process (Fig.1a). In Part I, segmentation techniques were discussed that searched for the global threshold values such that the resulting segmented image adhered the most to the measured data (Fig. 1b).While it was shown that this approach indeed resulted in more accurate images than by using conventional segmentation techniques, reconstruction artefacts (e.g.due to limited data) still defined a lower bound on the achievable accuracy
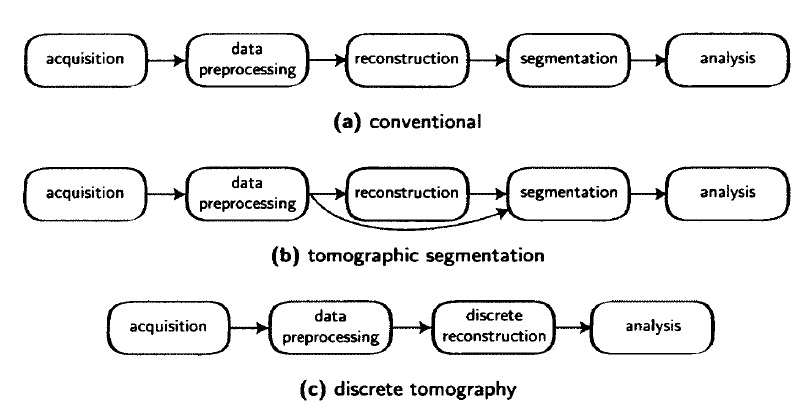
Figure1: (a) Conventional workflow of a typical tomographic application, (b) Workflow with tomographic segmentation, (c) Workflow with discrete tomography.