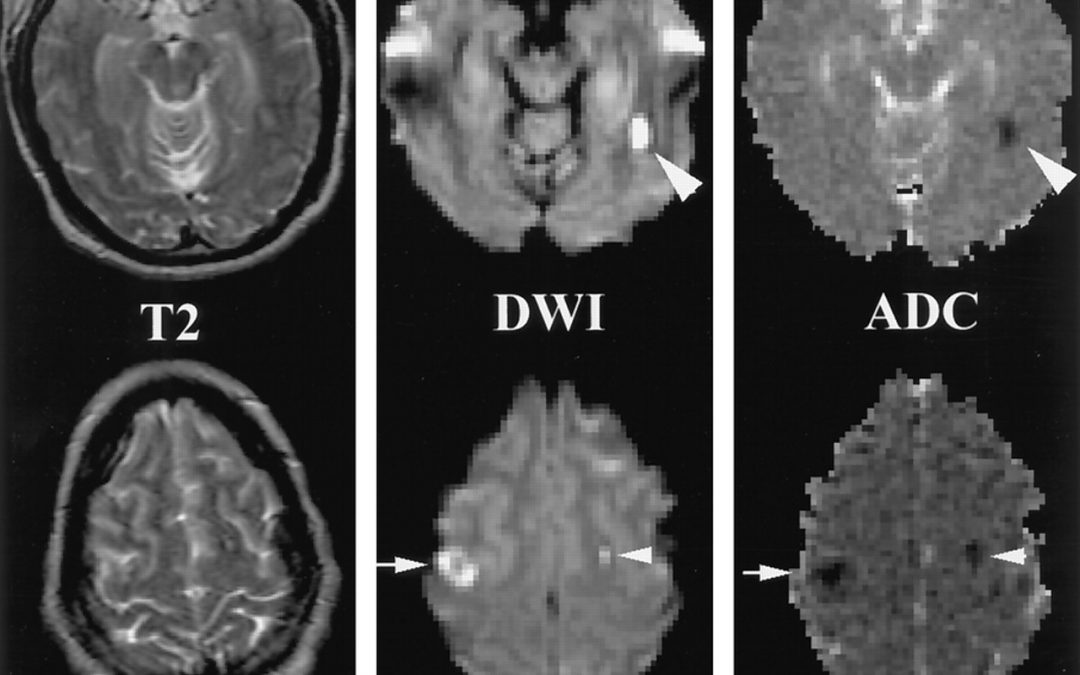
Diffusion Weighted Imaging
The free diffusion of water due to Brownian motion forms the basis for the development of diffusion MRI. In 1965 Stejskal and Tanner published a landmark paper describing an MR spin-echo pulse sequence that allowed the detection of the diffusion term in the Bloch-Torrey equation to obtain an estimate for the diffusivity of spins in a sample. In their sequence, nuclear spins of excited hydrogen nuclei are ‘tagged’ by adding spatially dependent spin phase with a gradient and at a later time they are untagged again by an opposite gradient (called diffusion encoding). For water molecules that remain in the same location during the process, the spatially dependent phase from diffusion encoding sums up to approximately zero at the point of MR (magnetic resonance) echo formation, but water molecules that moved between the tagging and untagging process retain a spin phase depending on the net distance they traveled in the direction of the gradient during that process. The effect of diffusion produces a reduction of the MR echo signal SD (with the diffusion un-weighted signal being S0) dependent o
From the log-difference between un-weighted and diffusion-weighted image divided by the b-value, the diffusivity can be calculated (equation 1.1a solved for D). The b-value depends on sequence related factors such as the duration δ of each diffusion encoding lobe, the time difference R between tagging and un tagging, the gradient strength G, and the gyromagnetic ratio γ. To account for anisotropies in human tissue which yield a different result of the DWI measurement every time the orientation of the imaging subject in the scanner is changed, diffusion images are typically acquired in three resulting measure is called the apparent diffusion coefficient (ADC) map. ADC measurements are typically calculated by prescribing two acquisitions of the imaged volume: one for a diffusion unweighted image, and another one weighed at a non-zero bvalue, typically around 1000s/mm2, which allows for sufficient diffusion contrast in an acceptable timeframe. Other methods of ADC calculation take into account the multi-modal exponential signal decay that becomes apparent with high diffusion weighting, which is suggested to originate from diffusivity of different compartments within voxels.In white matter fiber bundles the diffusivity of water is primarily restricted to the direction parallel to the axonal fibers. The presence of cell membranes and myelin sheaths perpendicular to the fiber direction restricts the water diffusion in that direction and thereby reduces the ADC value. Therefore, the ADC map is a useful measure for microscopic changes of white matter structure: Necrosis and demyelination generally increase ADC, while tumor invasion and mass effects of tumors can decrease ADC. Another clinical application of DWI together with perfusion imaging (providing a measure for water perfusion in tissue ) is the assessment of the ischemic penumbra (tissue at risk for infarction that can potentially be salvaged after an ischemic event) in stroke patients, which is characterized by a decreased perfusion of tissue but an increased ADC.While DWI allows an assessment of microstructural tissue changes visualized on a macroscopic imaging resolution, it does not provide information about the direction of fiber bundles, or to characterize the changes in fibrous tissue caused by diseases by their directionality relative to fiber bundles (i.e. diffusivity increases orthogonal to fiber bundles are suggestive of demyelination). The lack of directionality also does not allow differentiating individual fiber bundles with similar fiber density from each other or to track fiber bundles between different locations in the brain.
Diffusion Tensor Imaging
Diffusion tensor imaging (DTI) was introduced by Basser, Mattiello and Le Bihan in 1994 based on prior work by Le Bihan on intra-voxel incoherent water motion. It is a mathematical description (the ‘tensor’, a convenient representation of an ellipsoid) of the directed diffusion of water molecules occurring in fibrous tissue, restricted in their random movement by structural barriers such as cell walls . Thedirectional component of tracking water diffusion caused by Brownian motion is an extension of the isotropic diffusion model described by Stejskal and Tanner in 1965.This directionality is achieved by applying diffusion gradients in different directions for each scan, thereby sampling the diffusion space. A minimum of six gradient directions is necessary to solve the diffusion equation for the tensor model. To account for fiber crossings (that can be thought as two overlapping ellipsoids within a single voxel) and avoid directional undersampling, a minimum of 12 gradient directions are necessary.Typically, 25 gradient directions are chosen in clinical imaging, with the practical minimum being 13 directions (the next uneven number after 12 to avoid co-linearities for tensor calculation ) is repeated multiple times for separate scanning blocks until thedesired signal-to-noise ratio (SNR) is achieved (the ”, ).Varying diffusion weighting dependent on spatial gradient direction allows calculating the deviation of the spatial diffusivity from isotropy, the anisotropy, and the spatial orientation of the described ellipsoid model.. Owing to its ability to show the direction of neural fiber bundles as a consequence of tracking mobile water in tissue, DTI has proven itself to be a valuable complement to anatomical magnetic resonance imaging (MRI) studies for presurgical planning of brain-tumor excisions and is currently the only non-invasive in-vivo method to image white-matter fiber bundles. Different from other non-invasive in-vivo methods it is capable of providing an image of the spatial orientation of fiber bundles, probing the microscopic structural composition of axonal fiber directions and their density on a macroscopic imaging scale