Transient Acoustic Signal Detection and Classification
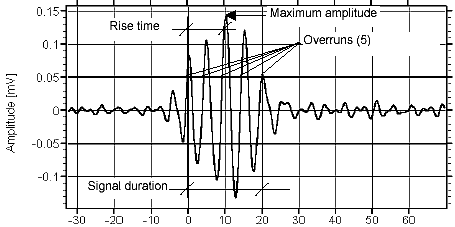
Features of transient signals
there are many challenges to detection and classication of transient acoustic signals. Due to the reasons stated earlier, there are only a few methods which could work for detecting and classifying man-made sources in national parks. Commonly, transient detection is done by having a model for observations when no transient signals are present (null hypothesis) and then looking for changes in the observed data which do not t this model . Once a transient signal is detected, Hidden Markov Model (HMM)-based classication schemes are often used to classify them as these models can deal with signicant data variability and easily model complex dependencies between consecutive observation vectors which are often found in many transient signals. For instance in , the authors break up a speech signal into overlapping 20 ms frames and perform an 8th order Linear Predictive Coding (LPC) analysis on each frame to create a 12-dimensional Cepstral vector representing each frame. These vectors are then used as inputs into discrete HMMs,which were trained on similar data, to determine the one that best ts this particular test sequence. In , the authors use a similar approach to classify objects from sonar returns. They formed feature vectors from overlapping segments of the data and used these vectors to train and test HMM models. The authors tested various techniques for extracting feature vectors from these frames including performing short time Fourier Transform (STFT) on the frames, fitting an auto regressive model to the observations in the frames and using the coeffcients of the model as the feature vector, as well as using wavelet coeffcients obtained by taking the wavelet packet transform of the frames. The class labels were decided based on which HMM model produced the highest likelihood ratio when applied to the test data. The problem with the HMM-based classication methods is that they are very susceptible to structured interference as they assume only one of the transient signals modeled by the HMMs is present in the data. This makes them almost useless in this type of application where strong interference (e.g., rain, thunder, wind) is often present. In , the authors attempted to remedy this problem by modeling the background interference as an HMM that is always present and the sources as HMMs that may or may not be present. The authors propose 2 ways to detect the presence of the new signal. The first method combines the two (or more) superimposed transients into one by taking the Kronecker product of their state transition matrices. Then, the authors use a CUSUM (cumulative sum) procedure based on Page’s test in order to find the start and end times of the superimposed HMM signal. Once the log likelihood ratio of multiple superimposed signals being present vs only one signal being present as computed in this CUSUM fashion exceeds a pre-dened threshold then a detection is declared. While straight forward, this method becomes computationally intractable for HMM signal models with large numbers of states or multiple superimposed signals. The second proposed method assumes independence between the state sequences of the superimposed signals given the observation sequence. This method also allows for the detection of superimposed signals but is more computationally effcient than the first method allowing for multiple and/or more complex superimposed signals to be detectedwithout numerical issues. As with the first method, a CUSUM procedure is used with these independent signal models in order to detect the start and end of a superimposed HMM signal. While these methods do address the issue of interference being present during a source event, the proposed detection procedure assumes that there is some signal (source or interference modeled by an HMM) always present in the data. Again, this is not the case in our application as wind and other natural interference events occur sporadically and there are often quiet periods in the data where no source or interference is present. Furthermore, it requires the computation of a log likelihood ratio for each possible combination of source and interference(s) for each observation which can become computationally expensive if a lot of interference signals are considered which may be the case in our application depending on the location which is being monitored. There are also some methods that deal with transient detection and classication simultaneously. For example, the authors in proposed using a wavelet network to detect and classify transient sources. The wavelet network is a combination of a wavelet transform followed by an articial neural network with each wavelet coeffcient being an input to the neural network. The authors then split up the incoming data stream into consecutive data segments of the same size and apply these segments to the wavelet network which outputs a class label for a transient source that exists in the data. This approach, however, is not very useful for our application as it requires exactly one transient to be present somewhere inside each data segment and it does not allow for transients to span multiple segments. In our application, there is no guarantee that a transient signature is going to t neatly into a time window regardless of it’s size (due to unknown start and end times of the transient events) and it is almost guaranteed that there will not be a source present in every consecutive data segment. Another recently proposed detection and classication method applies a set of hierarchical likelihood ratio tests to each data vector to classify it . The parameters for these likelihood ratios are estimated using a Kalman Filter and the classication decisions for theindividual data vectors are combined to classify the events that span over multiple observations. Although this sequential random coeffcient tracking (SRCT) method was shown to have better performance when compared to a Gaussian Mixture Model (GMM)-based method , where the likelihoods of each observation vector under each hypothesis are modeled using a mixture of Gaussians, it still struggled with detecting sources in the presence of multiple interference signals as is sometimes the case in our particular application. An extension of the previously mentioned CUSUM method is the Sparse Coeffcient State Tracking (SCST) algorithm . This algorithm is able to isolate sources from interference signals regardless of the number of interference signals present and it is also able to model much more complex sources than the SRCT method . This method also makes use of probability ratio tests similar to the generalized likelihood ratio test (GLRT) to detect presence of sources in the data as well as assign class labels to detected events. However, unlike SRCT and the HMM based methods, SCST uses a Bayesian Network (BN) model for the sources of interest allowing for greater structural variation of the sources. This method also allows for many types of interference to be present simultaneously as it creates separate subspaces for source and interference classes and then nullies the parts of the incoming signal that lie in the interference subspace, thus removing interference present in the signal, before detection and classication is performed. Although slightly more computationally demanding, this method was shown to perform much better on acoustic data from national parks than the previously developed SRCT method and a standard GMM-based method.


