Q-learning

wavelet

Q-learning

Even the value iteration algorithm is not the solution to every problem especially where the cost and the transition probability functions are unknown a priori, so the value iteration algorithm can not be used to compute the optimal value function. Instead we need to learn it online, based on experience.
So, we need some model-free RL approach like Q-learning. The main advantage of Q-learning is that it is able to compare the expected utility of the available actions without requiring a model of the environment. The optimal action-value function (Q-function) can be defined as

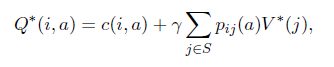
3

3

where V^*(j) is defined in (2). In words, Q^*(i,a) is the discounted cost achieved by taking action a in state i and following the optimal policy \pi^* thereafter. Using the action-value function, we can easily determine the value function

4

4

and the optimal policy

5

5

If the transition probability and cost functions are unknown, then the optimal action-value function can be learned according to the following algorithm known as Q-learning introduced byWatkins.

6

6

where i_n and a_n are the current state and action in time slot n, respectively, c_n is the corresponding cost with expectation c((i_n,a_n) and the next state i_{n+1} is reached in time slot n + 1, which is distributed according to p_{{i_n}{i_{n+1}}}(a_n)) is the greedy action in state i_{n+1}, which minimizes the current estimate of action-value function; \alpha_n \in [0,1] is a time varying learning parameter, \alpha_n=1/(n+1)^\omega, where \omega \in (1/2,1); and Q_0(i,a) can be initialized arbitrarily for all (i,a) \in S \times A. Now, the optimal Q can be written as,

7

7

Q^* can be learned by randomly exploring the available actions in each state. The convergence of this Q-learning algorithm can be easily shown following the approach in. The main theorem states that a well-behaved stochastic iterative algorithm converges in the limit and the lemma proves that Q-learning is a well-behaved iterative stochastic algorithm. But, before that we will just define the covering time and well behaved stochastic iterative algorithm.
Definition 2. Covering Time: Let \pibe a policy over a finite state-action MDP. Then covering time can be defined as the number of time-steps between t and the first future time that covers the state-action space S \time A (that is the MDP is covered) starting from any state i. The state-action space is covered by the policy \pi if all the state-action pairs are visited at least once under a policy \pi. An iterative stochastic algorithm is computed as:

8

8

where \om_n is bounded random variable with zero expectation, and each H_n is assumed to belong to a family of pseudo contraction mappings. Definition 3. An iterative stochastic algorithm is well behaved if: 1. The non-negative step size \al_nsatisfiesblank

2. There exists a constant G that bounds \om_n(i) for any history F_n i.e, n,i : |\om_n(i)|\leq G

3. There exists \ga \in [0,1] and a vector X^* such that for any X we have blank

Bertsekas and Tsitsiklis have already proved that the well-behaved stochastic iterative algorithm converges in the limit. Theorem 1. X_n being the sequence generated by a well-behaved stochastic iterative algorithm, X_n converges to X^* with probability 1. Lemma 1. Q-learning is a well-behaved iterative stochastic algorithm. So, from lemma 1, it is proved that Q-learning is a well behaved stochastic algorithm and then from theorem 2 the convergence of the Q-learning algorithm is proved.
Now, we would like to show the bound for the convergence time for the Q-learning algorithm derived in . Theorem 2. Let Q_n be the value of the asynchronous Q-learning algorithm at time n, then with probability at least (1-\delta) we have blankgiven that

9

9

where \be=(1-\ga)/2,|S| and |A| are the numbers of the states and the actions available in the set S and A respectively.
But unguided randomized exploration will not guarantee the best runtime performance because the sub-optimal actions can be taken frequently. By taking greedy actions, which exploit the available information in Q_n may lead to certain level of performance but will prevent the agent from exploring better actions. Though exploration is required because Q-learning assumes that the unknown cost and the transition probability functions depend on the action. Moreover, the Q-learning is not an efficient algorithm in the sense that it only updates the action-value function for a single stateaction pair in each time slot and does not exploit the known information.
As a result of this, Q-learning takes more time to converge to a near-optimal policy. So, the run-time performance suffers. To overcome this inefficiency of Q-learning, we can apply the so-called post-decision state learning algorithm which improves the run-time performance by exploiting the known information about system’s dynamics and enabling more efficient use of the experience in each time slot.

blank

Submit a Comment