1. From Power Networks to Smart Grids: Challenges vs. Opportunities
An intelligence revolution is happening in the technology of power networks (PN), supporting the development of so-called smart grids (SGs)1. Roughly speaking, “the term SG refers to electricity networks that can intelligently integrate the behavior and actions of all parameters and users connected to them” . This revolution transforms a traditional power grid from a singlelayer physical system into a huge cyber-physical network, using a layer of information that flows through the system (Figure 1). This information includes the status of several parameters in the network such as bus voltages, active and reactive powers, phase angles, branch currents, and load consumption, in addition to the actuating or controlling commands fed back to the network from controllers and decision making units . Another important feature of next generation SGs is the aggregation of renewable energy microsources in distributed generation technology . Despite the environmental advantages bring in by utilizing the renewable sources of energy, the nature of the injected power from renewables as wind turbines and solar panels is inherently random. This randomness, along with the uncertainty in the load, lead to probabilistic behavior in the load-power flow at buses . Collecting, transferring, and storing the huge amount of data flowing through the information layer of large scale SGs, together with the uncertainty caused by distributed power generators and load characteristics, challenge the standard methods for security, monitoring, and control. Other important issues are the time cost, efficiency and accuracy of real-time data analysis within these huge interconnected and complex networks . Nowadays, the Supervisory Control and Data Acquisition (SCADA) system reports the electrical parameters of buses almost within the range of couple of seconds. Moreover, Wide Area Monitoring System (WAMS) uses the data measured by phasor measurement units (PMUs) toreport the electrical parameters at the monitored buses by exploiting a global positioning system (GPS) for each local system in near real time . Currently, the system data exchange (SDX) module of the North American Electric Reliability Corporation (NERC) provides network-wide status on an hourly basis , however, to transform the PN into a smart network a near real-time monitoring of system status, in all the operational levels, is mandatory .
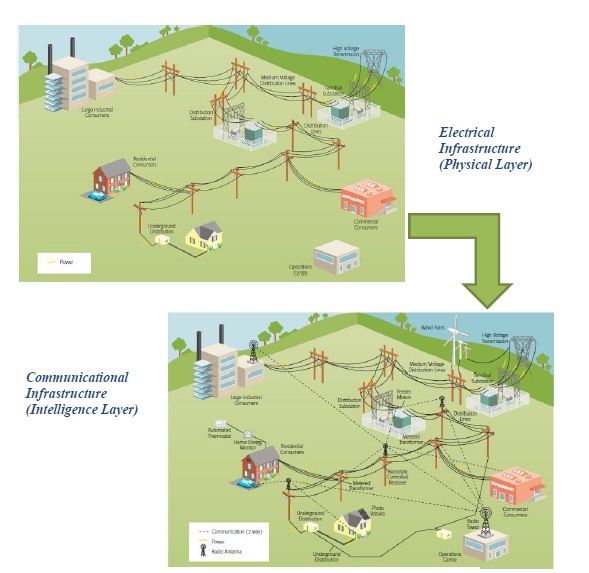
Figure 1. From Traditional Electrical Grid to Smart Grid
In terms of power engineering technology, we can split the monitoring challenges into two major groups: 1. Global or network-wide level problems, such as network topology identification, power system state estimation, and power line outage localization. 2. Local level or, the signal processing problems, this second category is mostly related to the power signals quality monitoring and analysis, such as nodal load or price estimation, electrical equipment monitoring, voltage and current disturbances detection and classification.
2. Full Observability from Partial Information
In general, most of the monitoring approaches, within local operational levels, are highly dependent on the quality of the available data from system parameters and poorly perform in case of corrupted measurements where only partial information may be available . On the other hand, most of the classical global level monitoring methodologies have been adapted in case of simple structures, these methods are usually suffering from high computational cost and nonlinearity in formulation which results in intractable solutions in case of real time applications . These computational issues are specifically highlighted in case of large-scale PNs, where usually a huge amount of data is arrived at the control and operational rooms in every time slot. In many practical cases (considering the time cost, storage capacity limitations and power efficiency), operators may have to intelligently reduce the amount of data needed to be processed and still accurately extract the whole of the useful information for system analysis applications. These inherent technical challenges motivated us to investigate the applications of Compressive Sensing and Sparse Recovery (CS-SR) in the analysis of smart power networks to deal with the big data analysis issues in SGs. Compressive sensing is a new technique in signal processing that has revolutionized the data analysis science. Due to its time efficiency, the CS-SR framework has found a critical role in the large scale data/system modeling/analyzing and significantly affected the era of Big Data. From the signal processing viewpoint, CS is a novel sensing/sampling technique that abjures the prevalent wisdom in signal and data acquisition. Based on the Shannon sampling theorem and regarding the Nyquist sampling rule, the minimum sampling frequency (number of samples per cycle) needed for capturing the complete information from a phenomenon should exceed two times of the phenomenon bandwidth (please also refer to ). Roughly speaking, the CS theorem tries to answer the following question:
Can a sensor be designed that records fewer samples of a very high dimensional signal (? ∈ ℝ?), while missing information (or samples) can be reconstructed from the collected ones?
The answer is yes if the phenomenon under study has an inherent information level that could be well modelled utilizing only ? parameters or degrees of freedom2. A comprehensive study in CS literature has revealed the fact that practically most of the natural and industrial ?-sample signals have far smaller than ? degrees of freedom. This fact suggests that, under appropriate conditions, one may exploit the signal’s information level ? instead of its ambient dimension ?, to design an efficient measuring, and modeling framework for high-dimensional signal analysis. In other words, the fundamental idea that underlies CS-SR theorem is that ‘if a signal has an intrinsic information level ? it can be possible to record a small number of linear measurements of the signal, ?, proportional to ?3; “compressive sensing”, and from those measurements reconstruct the complete set of all, ?, samples that a conventional sensor would have recorded, “sparse recovery”’ as stated in . Not only low dimensional behavior can be captured in many real-world signals, but also many system models rely on a low dimensional (sparse) structure. This idea has been further developed and resulted in arising of a new branch in the CS-SR field, widely known as Compressive System Identification (CSI), as termed in , where an inherent sparsity can be observed in the system structure/model, or when a typical problem represents a sparse behavior in its formulation. In compressive systems, the sparse recovery techniques can be utilized to address the large-scale system modeling problems in a fast and time efficient manner. A famous class of CSI problems is related to graph structures analysis. Intuitively, a sparse recovery problem (SRP) is an optimization problem in which the goal is to recover a ?-sparse signal ??ℝ? from a set of observations ? = ?? ?ℝ? where ??ℝ?×? is the sensing protocol (matrix) with ? < ? (in many cases ? << ?) . Due to the underdetermined nature of this recovery problem (since ? < ?), the null space of the matrix ? is non-trivial; therefore, there exist infinitely many candidate solutions for this problem. However, under certain conditions on the sensing matrix ?, various sparsity based recovery methods can be guaranteed toefficiently find the candidate solution that is sufficiently sparse. Examples of such conditions are the restricted isometry property (RIP), the exact recovery condition, and low coherence . In essence, what these conditions require is that any two small subsets of columns of the sensing matrix ? must be almost orthogonal to each other.
3. Complex Structure but Sparse Nature of Power Systems
At first glance, most of the power networks, either in the transmission or in the distribution level, may look like a huge interconnected system with a high level of complexity and extensive number of electrical parameters. However, most of these systems are less complicated than what is suggested. For example, in terms of transmission networks, one may easily figure out most of the standard PN models are forming a sparse interconnected graph. This sparsity in the structure helps us to reformulate the power network topology identification as a sparse recovery problem that can be solved using a small set of measurements in a fast and accurate way using sparse recovery solvers . This sparsity assumption can be proved based on our observations on a survey of standard power grid models found on databases and toolboxes such as MATPOWER . Considering a variety of standard PN models, it can be observed that the regular maximum connectivity level of an electrical bus in a grid is typically less than 5-10%, especially in case of large-scale PNs . As suggested in , the same fact can be, more or less, observed in case of distribution networks as well. Now we discuss another possible sparse monitoring problem where the fact of sparsity is not easily observable from the beginning. In the network-wide operational level of SGs, fast and reliable localization of power line outages is categorized on top of the critical tasks. Power line outages can result in heavy damages such as blackouts , while massive blackouts can be prevented if we have a comprehensive situational awareness of the structure of the power grid. Initially, one may not be able to figure out a sparsity in the power line outage detection problem, however, there is an inherent sparsity pattern in this problem, that is in the most of the practical scenarios the number of simultaneous outages may happened within a power network is a very small portion of the total number of active transmission lines . Consider a PN with a set of ? transmission lines, assume a set (????) of ?0 lines have been damaged within a failure phenomenon in the network. Assign an outage index to each line and collect them in an outage vector ? ∈ ℝ? where ?? ??? ? = 1: ? is equal to 1 if ? ∈ ???? and 0 otherwise. Obviously, the corresponding outage vector ? would have a sparse structure with most of its elements equal to zero except for those on the corresponding outage locations. Thus, one may think of developing a possible formulation where the outage vector ? can be recognized using a set of measurements from network parameters . A variety of other possible sparse recovery-based applications may also be revealed in the global monitoring level problems by manipulating the mathematical formulation of power systems models. On the other hand, in the local monitoring level, we majorly face with the power signal analysis problems for sake of stability and protection. Naturally, most of the electrical signals (such as currents and voltages) are traveling through the power systems in the shape of a single-frequency sinusoidal wave. Due to system variations, such as load uncertainties, this fundamental sinusoidal shape may temporarily (such as impulsive events during arcs) or steadily (such as long term harmonic integrations) change during the time. However, it can easily be shown that under almost all operational conditions a typical time segment of a power signal can still be sparsely represented in terms of another signal domain (such as frequency domain). As a result, one may exploit this natural sparsity to address the power signals analysis in terms of a CS-SR problem to reduce the time cost and improve the system reliability for online applications.


