Greedy algorithms estimate the support and coefficients of the signal in an iterative approach. At each iteration the estimate of the signal is improved by updating its support. Two well know Greedy algorithms are Matching Persuit (MP) based methods and Iterative Hard Thresholding (IHT) . MP is based on updating the dictionary at each iteration by adding the vectors on which the residual has the largest projection. Then, the selected vectors of the dictionary are removed from the residual and this is repeated until the norm of the residual is smaller than a preset threshold. The pseudo-code of an Orthogonal Matching Persuit (OMP) algorithm is shown in Algorithm 2 . At each iteration it finds the most correlated column of the measurement matrix with the measurement residual and adds it to the support. In this algorithm A† is the Moore-Penrose pseudo inverse of A.

Algorithm 2 Pseudo-code of Orthogonal Matching Persuit
OMP has been improved and extended by Stage-wise Orthogonal Matching Pursuit (StOMP) , and Compressive Sampling Matching Pursuit (CoSaMP) , which allow multiple coefficients to be added to the support at each iteration with tighter bounds on convergence and performance. Iterative Hard thresholding is a simple and straightforward algorithm consisting of a gradient descent update followed by hard thresholding applied iteratively until the stopping criterion is met. Pseudo-code of the IHT algorithm is given in Algorithm 3. In this pseudo-code Hk(x) is a hard thresholding functional, which keeps the largest k entries and maps the smaller elements to zero.
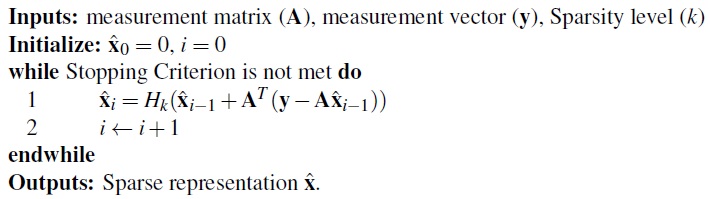
Algorithm 3 Pseudo-code of Iterative Hard Thresholding

