Beamforming and Source Tracking
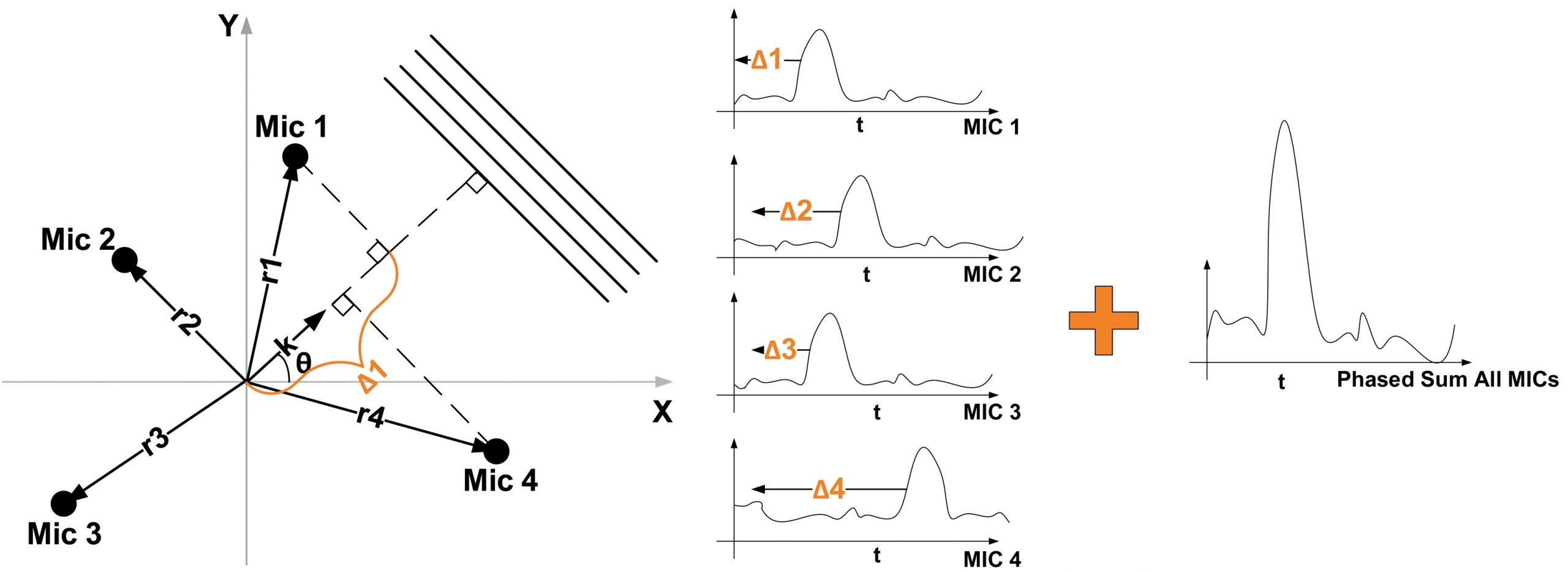
figure 1 . the output of each microphone in an array is shifted and then added to amplify sound signals arriving from a specific direction
Once a source is detected and classified, the system will need to generate the trajectory of the moving source. Since only acoustic data is available for this purpose, a beamforming algorithm will need to be used to estimate the direction of arrival (DOA) angle of the acoustic source relative to the microphone array and these DOA estimates will then need to be used to create the trajectory of the moving source. Since all of the sources of interest occupy a large range of frequencies, a wideband beamforming algorithm will need to be employed for this purpose. Wideband beamforming algorithms use sensor array processing to determine the DOA of a signal based on the time delays at which each element in the array recorded the signal. Some of the popular wideband beamforming algorithms include wideband extensions of the multiple signal classication (MUSIC) algorithm , steered covariance matrix (STCM) algorithm , and weighted subspace fitting (WSF) algorithm . MUSIC is an algorithm used to find the DOA estimates of multiple sources from the spatial covariance matrix of the observations. It is thus inherently a narrowband beamforming technique though it can easily be extended to wideband DOA estimation using coherent or incoherent averaging methods . Although this algorithm does perform better when estimating DOAs than simply picking peaks in power spectra of a beamformer, it requires the computation of eigenvalues and eigenvectors of spatial covariance matrices and also the a priori knowledge of the number of sources and structured interference present in the observed data. Since we do not have this a priori knowledge in our application and finding eigenvectors and eigenvalues of spatial covariance matrices would require far more computational resources than we can spare, the MUSIC algorithm is ill-suited for our application. In STCM, the covariance matrices for each narrowband component are pre- and post-multiplied by transformation matrices before being summed together to form a single focused covariance matrix. This coherent beamforming method works better than incoherent averaging methods when the SNR is low. However, this method has additional computational requirements compared to incoherent averaging methods due to the need to compute and use transformation matrices when forming the focused covariance matrix . Furthermore, it was shown that under certain SNR conditions the incoherent methods produce more accurate DOA estimates for highly peaked spectra when compared to coherent methods so this additional complexity might not be warranted depending on the application.The WSF method , on the other hand, finds the DOA estimates by solving a system of homogeneous non-linear equations based on the eignevalue decomposition of the narrowband covariance matrices. It involves a minimization problem which may contain multiple local minima and thus does not guarantee that the correct DOA angles will be found. This method requires more computations than the STCM method and also is not guaranteed to produce good results for the DOA estimates making it a poor candidate for implementation on our sensor board system. To address the issues with the previously mentioned methods, the authors in proposed an incoherent extension of the Capon beamformer to the wideband case using various averaging techniques including geometric, arithmetic, and harmonic averaging. They showed that the geometric averaging variant produced the narrowest beampattern out of all the wideband Capon variants thus allowing for the best DOA resolution of a source while maintaining the computational demands at a manageable level. This DOA estimation method is thus ideal for implementation on our sensor board as it requires the fewest computations out of all the previously mentioned methods while at the same time provides DOA estimates that are accurate enough for our purpose.


