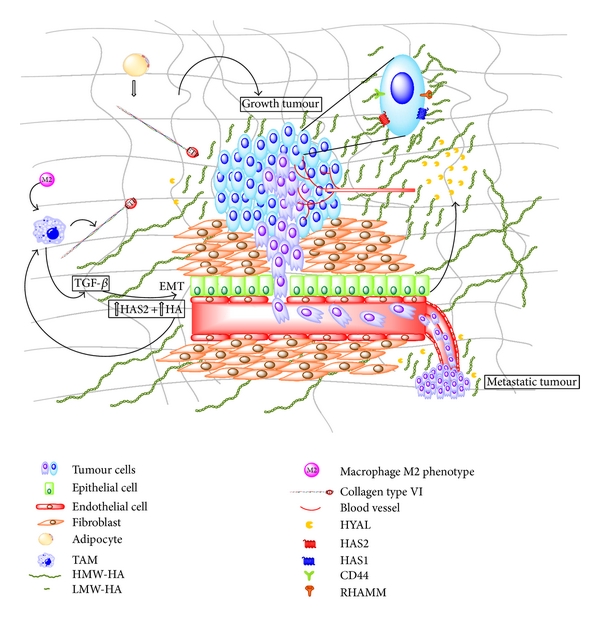
The interaction between cells and extracellular collagen I plays an important role in maintaining normal cell behavior , and the disruption of this interaction is one of the hallmarks of the transition from in normal tissue to malignancy (Figure 1). It is still not clear if the breakdown of structure precedes or follows the invasive transition, but it has been shown that overexpression of an ECM remodeling enzyme, matrix metalloproteinase 3 (MMP-3), stimulates the establishment of a reactive stroma which is characterized by increased deposition of collagen I prior to tumor formation . MMP-3 has also been shown to promote reactive stroma and fibrosis, leading to carcinogenesis in murine mammary glands . The increased deposition of collagen I, characteristic of a reactive stroma, is just one of several specific collagen I structural changes found in the presence of mammary tumors. These changes we call Tumor Associated Collagen Signatures (TACS) fall roughly into three categories: (Table 1, Figure 2)

Figure 1: SHG images of normal murine mammary tissue (left) and murine mammary tissue surrounding a tumor (right)


Figure 2: Graphical representations of tumor associated collagen I structures as described in Table 1. A-B) Category I C-D) Category II, E-F) Category III
Digital Signal Processing
The images resulting from these microscopy techniques can be quantitatively analyzed using methods based on digital signal processing. A signal can be defined as a description of the way that the behavior of one process or parameter depends on another. This relationship is typically represented as a mathematical function of one or more independent variables. A one-dimensional signal, such as an audio signal, consists of an independent variable, which commonly represents time, distance, etc., and a dependent variable, which is a function of the independent variable (Figure 4). If the independent variable occurs over a range of continuous values, then the signal is said to be a continuous signal. If the independent variable occurs over a range of discrete values, then the signal is a discrete or digital signal. For a digital signal, the independent variable describes the sampling of the process and the dependent variable is the value of each sample.
The independent variable can also be said to define the domain of a signal. A signal for which the independent variable represents time is a time-domain signal. Likewise, a signal for which the independent variable represents distance or frequency is known as a spatial-domain or frequency-domain signal, respectively. A fundamental area of digital signal processing deals with mathematical techniques for converting signals from one domain to another. The Fourier transform is a well-known example of these techniques, and is used to convert time-domain signals into frequency-domain signals.The images resulting from these microscopy techniques can be quantitatively analyzed using methods based on digital signal processing. A signal can be defined as a description of the way that the behavior of one process or parameter depends on another. This relationship is typically represented as a mathematical function of one or more independent variables. A one-dimensional signal, such as an audio signal, consists of an independent variable, which commonly represents time, distance, etc., and a dependent variable, which is a function of the independent variable (Figure 4). If the independent variable occurs over a range of continuous values, then the signal is said to be a continuous signal. If the independent variable occurs over a range of discrete values, then the signal is a discrete or digital signal. For a digital signal, the independent variable describes the sampling of the process and the dependent variable is the value of each sample

Figure 4: Example of a 1D digital signal. The x-axis describes the sampling of the process and the y-axis is the value of each sample.
