An introduction to indexing in MATLAB
All variables in MATLAB are arrays, so to work with MATLAB we need to know how to work with arrays. In solving various problems with MATLAB, it often happens that we need the following two features:
To extract a specific element from an array. This is called indexing.
Or extract a specific part of an array. This is called slicing.
In this session of free MATLAB training, we want to examine how to index in MATLAB.
Familiarity with indexing in MATLAB and slicing in MATLAB
Let’s start the definition of indexing and slicing in MATLAB with an example. Imagine for a second you were transposed into the karmic driven world of Earl. Now you want to tell the seller which sweets you want. This is while you do not know the name of any of the sweets. The salesperson asks you which sweets you want. what do you say? For example, you say that the candy in the third row and from the left of the second column catches my eye, and it often happens that in coding we want to point to an element of the array. We use the same method to point to an element of an array! This type of addressing in MATLAB is called indexing. How we do this, stay tuned فع
You may be familiar with working with matrices and indexing in high school and college math in matrices. Yes, indexing in MATLAB is similar to the matrix in mathematics. Of course with a host of advanced techniques…
Maybe you are very interested in sweets and want to buy more sweets. This time, in response to the seller’s question, what sweets do you want to say? For example, you say I want the third row whatever it is. Or I want all the sweets in the first column from the right. In coding, it also happens that we want to extract several elements together from an array. This is called slicing in MATLAB.

indexing MATLAB
Vectors and indexing in MATLAB
As we said, referring to an element of an array is called indexing or indexing. We start with the vector. To refer to an element in a vector, it is enough to know that it is multiple elements. Let us first define a random line vector. Consider a vector length of, for example, 9:
>> x = randi(20, 1, 9)
x =
2 2 11 16 19 3 12 10 1
If you forgot how to use randi in MATLAB, go back to the random matrix session in MATLAB and browse. So we have a line vector of length 9 called x. Now we want to point to the number 19. We said it is enough to know that the number 19 is a multiple of a number. It’s the fifth number, right? To refer to this number, it is enough to write:
>> x(5)
ans =
19
So to point to an element of the vector, we find the number of that element. Then we write the name of the variable and in front of it, enter the number of that element in parentheses and press Enter. The element number in coding is called an index. We do exactly the same thing for column vectors. Let’s check. First, define a random column matrix of length 4:
>> y = randi(10, 4, 1)
y =
4
2
8
4
What should we do to point to the number 8? We have to find its index. What is Index 8? True 3. So to point to 8 we write:
>> y(3)
ans =
8
Matrix and indexing in MATLAB
We know that a matrix has one more dimension than a vector. The vector is a one-dimensional array and the matrix is a two-dimensional chariot. How is indexing in the matrix with these conditions? How to refer to an element of the matrix? First, let’s define a random matrix. Define a 3 in 4 random matrix and assign it to the variable z:
>> z = randi(15, 3, 4)
z =
8 4 12 4
3 10 7 14
10 11 2 3
So how can we point to an element here? This is possible in the same way as before. That is, enter the element number again. But how do we know which side to count? Count from left to right or up and down? MATLAB indexes the elements of a matrix as follows:
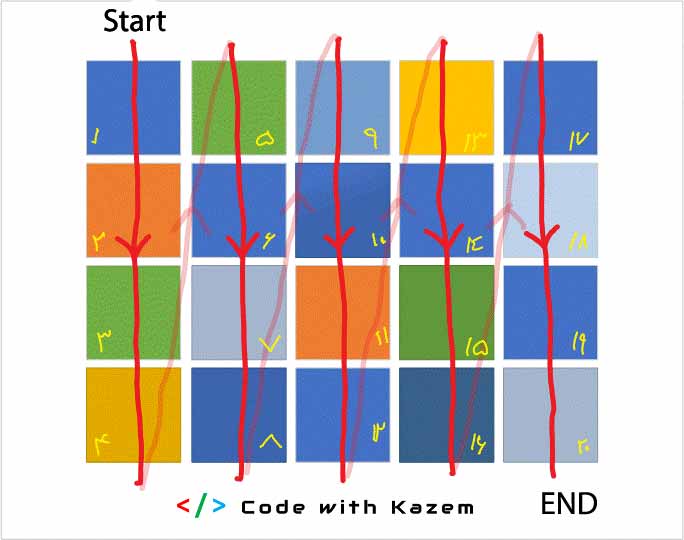
indexing MATLAB direction
Look at the yellow numbers in the picture above. These numbers show how to index the MATLAB matrix. For example, in the z matrix that we defined, the number 7 becomes a multiple of how many? The eighth number, right? Well now we write:
z =
8 4 12 4
3 10 7 14
10 11 2 3
>> z(8)
ans =
7
Well we were able to extract the number 7. But finding its index was a little hard, wasn’t it? Now what if we had a larger matrix? For example, if we had a 20-by-20 matrix, finding an index is a difficult task. How many times do we sit down and multiply what the index of the number we want is! MATLAB has thought about this as well. There is another way to index matrices in MATLAB. In this method, instead of using the element number, the row and column number of that element is used. This method of indexing is more common for matrices. Well, in this method, it is enough to find the row and column numbers of the element. Take a look at the image below. The number of rows and columns in the matrix in MATLAB is listed as follows:

Matrix direction indexing
For example, in the above matrix, a11 is its index (1 and 1). That is, the first row and the first column. This point is the starting point in the matrix. Another example is a32 in the third row and second column. That is (2 and 3). Now let’s go to matrix z… Do this for the number 7 in matrix z. As you can see, this number 7 is in the second row and the third column of the z matrix. Now how do we use these numbers? To index rows and columns, just write:
>> z(2, 3)
ans =
7
So we entered the row number first and then the column number. Exactly what we did in choosing the sweets! Well, so far we have become familiar with the indexing of vectors and matrices. In the next section, we will get acquainted with an important keyword in indexing in MATLAB.
Note: As we said before, enter the first row next to column… for the index in MATLAB, the first row next to the column.
Note the two methods for indexing in the matrix were mentioned. One vector-like method and the other line-column method both work and learn both. But in matrix indexing, the row-column method is often used.
Use end in indexing in MATLAB
We saw that to move rows and columns in MATLAB, we move from top to bottom and left to right, respectively. But see what features MATLAB has given you to point to the last row or column, and you can use the end keyword to point to the last element of each row or column. For example, if we want to refer to the last row and the second column of the variable z. In this case, it is enough to write:
>> z(end, 2)
ans =
11
>> z(3, 2)
ans =
11
Whether we use the end or exactly the number to refer to the last line, the result is the same. But with the end, our work becomes a little easier to point to the last rows and columns. You can also use the end keyword to refer to elements before the end! That is, for example, you can use end to point to the last column left. All you have to do is write end-1. You can also extract earlier elements. For example, if we want to extract the element that exists in the last row of rows and the last row of dual columns from z. In this case, we write:
>> z(end-1,end-2)
ans =
10
Slicing in MATLAB
Slicing in MATLAB means selecting a part of a matrix or vector. For example, if we extract elements 2 to 6 together in a vector, this is called slicing. In MATLAB slicing, the Cullen (:) operator plays an important role. In the following, we will introduce this operator and examine how to do slicing together.
The Cologne operator (:) is the distance symbol. In fact, this operator represents the word “until”. We said we want elements 2 to 6 in a vector. This is translated into MATLAB phrase 2: 6. Let’s go to coding and learn more. Let us extract elements 2 to 6 from the vector x using the Coulomb operator:
>> x
x =
2 2 11 16 19 3 12 10 1
>> x(2:6)
ans =
2 11 16 19 3
Check to see if it is correct. We can also do this for indexing matrices. For example, suppose we want to extract the elements of the first row and columns 2 to 4. In this case we must write:
>> z(1, 2:4)
ans =
4 12 4
Let’s combine the Cullen operator with the end keyword. For example, suppose we want to extract the elements 4 to the end of the vector x. In this case we must write:
>> x(4:end)
ans =
16 19 3 12 10 1
MATLAB indexing and slicing practice in MATLAB is a game and math. You have to practice a lot to master them. So please do not forget to practice…
Change array values with index in MATLAB
The elements of an array can be changed by combining indexing and value assignment. In this way, we first extract the element or elements we want using indexing. Then we equate these elements with the new values. For example, suppose we want to replace the value of 19 in the vector x with 44. In this case, it is enough to write:
>> x(5) = 44
x =
2 2 11 16 44 3 12 10 1
You can see that 44 replaces 19 in index 5. Similarly, for matrices, values can be changed by indexing. You can also change the values of several elements together. For example, suppose we want to replace the elements in the first row and columns 2 to 4 of z with the values 1, 1, and 1. In this case we must write:
>> z(1, 2:4) = [1, 1, 1] z = 8 1 1 1 3 10 7 14 10 11 2 3
We extracted the elements we wanted and then replaced them with new values. Note that it is better to convert these values into a vector. That is, it is better to convert the values 1, 1, and 1 into vectors [1, 1, 1], which we did the same.
Note There is another important point about the Coulomb operator. The Coulomb operator is also used to select all elements of a row or column. For example, if we want to select all the elements in the third line of the variable z, it is enough to write:
>> z(3, :) ans = 10 11 2 3
Trick If you just give a matrix, the index: something interesting will happen. For z we do this:
>> z(:)
ans =
4
8
3
10
10
4
11
12
2
7
14
3
You see, by doing this, the matrix z becomes a columnar vector! Sometimes we need to convert a matrix to a vector. We have told you one way, we will talk more about these conversions later.
sd
